Министерство транспорта Российской Федерации
Федеральное агентство железнодорожного транспорта
Омский государственный университет путей сообщения
_____________________________________________________
И. А. Дроздова, Г. Б. Тодер
ЗАКОНЫ СОХРАНЕНИЯ В МЕХАНИКЕ
(ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ)
Утверждено редакционно-издательским советом университета
в качестве методических указаний для самостоятельной работы студентов
при решении задач по физике
Омск 2009
УДК 530.1(075.8)
ББК 22.3
Д75
Законы сохранения в механике (примеры решения задач): Методичес-кие указания к решению задач по физике / И. А. Дроздова, Г. Б. Тодер; Омский гос. ун-т путей сообщения. Омск, 2009. 38 с.
Приведены краткие теоретические сведения по теме «Законы сохранения в механике», примеры решения типовых задач на применение законов сохранения импульса, момента импульса и энергии в механике материальной точки и абсолютно твердого тела, которые должны уметь решать студенты согласно требованиям учебной программы.
Предназначены для студентов первого курса технических вузов дневной и заочной форм обучения.
Библиогр.: 6 назв. Табл. 1. Рис. 14.
Рецензенты: доктор техн. наук, профессор В. А. Нехаев;
канд. физ.-мат. наук, старший преподаватель А. А. Печерицын.
__________________________
© Омский гос. университет
 путей сообщения, 2009
путей сообщения, 2009
Введение1 1 5
1. Краткие теоретические сведения11 6
2. Примеры решения задач1 11
2.1. Работа. Энергия. Закон сохранения энергии1 11
2.2. Закон сохранения импульса1 15
2.3. Закон сохранения момента импульса29
Библиографический список1 38
 |
При изучении курса физики решение задач имеет большое значение, поз-воляет лучше понять и запомнить основные законы физики, развивает навыки в применении теоретических знаний для решения конкретных практических воп-росов.
Цель настоящих методических указаний – оказать помощь студентам в освоении методики решения типовых задач по теме «Законы сохранения в механике».
Такие величины, как работа, энергия, импульс, момент импульса, и соот-ветствующие законы сохранения в механике играют важную роль в физике, так как связаны с симметриями пространства – времени. В задачах, решения которых представлены в данном издании, эти величины определяются, а законы применяются при вычислениях в рамках механики материальной точки и абсолютно твердого тела. Краткие теоретические сведения, необходимые для решения задач, приведены в настоящих указаниях, а теоретические сведения в полном объеме содержатся в книгах [1 – 6].
При решении задач с применением законов сохранения рекомендуется следующий порядок действий: 1) определить, какие состояния механической системы необходимо рассмотреть в данной задаче, и для каждого состояния сделать рисунок; 2) определить, какие законы сохранения являются существенными при переходе системы из одного состояния в другое по условиям задачи, и записать эти законы; 3) решить полученную систему уравнений, используя данные задачи.
Все задачи следует (по возможности) решать в общем виде. Это означает, что сначала выводится формула для расчета искомой величины, а затем в нее подставляются численные данные. Такой подход позволяет при анализе полученных формул увидеть общие закономерности. Прежде чем приступить к решению, следует внимательно прочитать, обдумать и записать условия задачи, перевести единицы измерения всех величин в основные единицы СИ, сделать схематический рисунок, отражающий условия задачи, выбрать подходящую систему отсчета. При вычислениях рекомендуется применять формулы приб-лижения, позволяющие упростить расчеты.
Для решения задач механики важнейшими характеристиками
движения механических систем являются кинетическая энергия ![]() импульс
импульс ![]() момент
импульса (момент количества движения, кинетический момент)
момент
импульса (момент количества движения, кинетический момент) ![]() а мерами действия силы – импульс силы
а мерами действия силы – импульс силы ![]() работа
работа ![]() и
момент силы
и
момент силы ![]()
Материальная точка массой ![]() движущаяся
относительно инерциальной системы отсчета со скоростью
движущаяся
относительно инерциальной системы отсчета со скоростью ![]() имеет
кинетическую энергию
имеет
кинетическую энергию
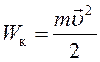 ,
(1.1)
,
(1.1)
импульс ![]() момент количества движения
момент количества движения ![]() где
где ![]() –
радиус-вектор точки.
–
радиус-вектор точки.
Полная механическая энергия системы равна алгебраической сумме механических энергий материальных точек, входящих в нее:
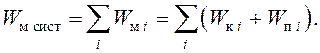 (1.2)
(1.2)
Полный импульс системы равен векторной сумме импульсов материальных точек, входящих в нее:
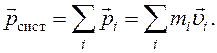 (1.3)
(1.3)
Полный момент количества движения системы равен векторной сумме моментов импульса материальных точек, входящих в нее:
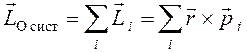 ,
(1.4)
,
(1.4)
Абсолютно
твердое тело, вращающееся вокруг неподвижной оси ![]() с
угловой скоростью
с
угловой скоростью ![]() имеет кинетическую
энергию
имеет кинетическую
энергию
 (1.5)
(1.5)
и момент импульса относительно оси вращения
![]() (1.6)
(1.6)
где
![]() и
и ![]() –
момент инерции тела относительно оси
–
момент инерции тела относительно оси ![]() и проекция угловой
скорости тела на ось
и проекция угловой
скорости тела на ось ![]() соответственно.
соответственно.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.