Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 4

Благодаря применению законов сохранения оказывается возможным решение задач на взаимодействие тел в случаях, когда характер сил взаимодействия неизвестен. Однако прежде чем применять закон сохранения, необходимо убедиться в том, что рассматриваемая система является именно той, в которой данный закон выполняется. Следует обратить внимание также на то, что все характеристики, входящие в уравнения, составленные на основании законов сох-ранения, должны рассчитываться относительно одной и той же инерциальной системы отсчета.

2. ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ

2.1. Работа. Энергия. Закон сохранения энергии

Задача 1. Тело бросили с поверхности Земли вертикально вверх со ско-ростью 980 см/с. Пренебрегая силой сопротивления воздуха, найти, на какой высоте кинетическая энергия тела будет в четыре раза больше потенциальной. Потенциальную энергию тела в точке бросания принять равной нулю.

Дано:  = 980 см/с Fсопр= 0	СИ 9,8 м/с	Решение.
- ?

По условию задачи силой сопротивления воздуха можно пренебречь, следовательно, на тело действует только сила тяжести, являющаяся консервативной, и выполняется закон сохранения механической энергии:

,                                                      (1)

где  - полная механическая энергия тела в начальном состоянии (в мо-мент броска) (рис. 2.1, а),

;                                                 2)

 – полная механическая энергия тела в момент положения центра тя-жести на искомой высоте (рис. 2.1, б),

                                              (3)

Подставив в формулу (1) равенства (2) и (3), получим:

                                        (4)

По условию задачи в момент броска кинетическая энергия 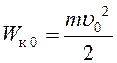, , на искомой высоте , потенциальная энергия , где – масса тела. Подставив эти соотношения в формулу (4), получим:

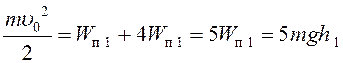.                              (5)

Отсюда

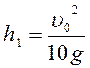.                                                      (6)

Подставим в формулу (6) данные задачи:  м.

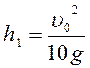Ответ: ;  м.

Задача 2. Диск радиусом 17 см вращается под действием постоянной касательной силы 50 Н вокруг оси, проходящей через центр диска перпендикулярно его плоскости. Найти работу этой силы, совершенную в течение трех оборотов диска.

Дано: см = 50 Н  = 3	СИ 0,17 м
- ?

    Решение.

Работа постоянной силы при вращательном движении определяется по выражению:

,                                      (1)

где j - угол поворота (за один оборот абсолютно твердое тело поворачивается на угол 2p),

;                                      (2)

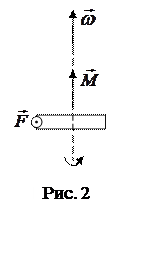
 – проекция момента силы на направление угловой скорости . Так как по условию задачи вращение диска происходит под действием силы  момент силы  (рис. 2), следовательно,  Так как сила касательная, модуль момента силы , поэтому

.                                    (3)

Подставив выражения (2) и (3) в формулу (1), получим:

.                                                     (4)

Выполним численный расчет по формуле (4):  Дж.

Ответ: ,  Дж.

Задача 3. Однородный цилиндр скатывается без скольжения с наклонной плоскости высотой 30 см. При скатывании ось цилиндра все время сохраняет свое горизонтальное положение. В начальном состоянии цилиндр покоился. Найти скорость центра инерции цилиндра у основания плоскости. Потерями энергии за счет тормозящих сил пренебречь.

Дано:  см  = 0	СИ 0,30 м
- ?

Решение.

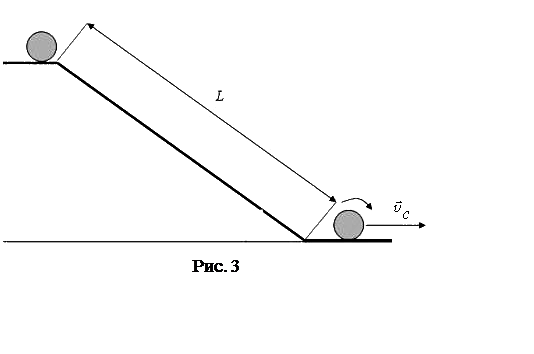
Будем отсчитывать потенциальную энергию цилиндра в поле тяжести Земли от основания наклонной плоскости (рис. 3). Тог-да механическая энергия цилиндра в начальном состоянии (в состоянии покоя) и у основания плоскости в конце скатывания определяются по формулам соответственно:

                                                      (1)

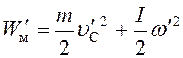,                                               (2)

где m,   – масса, угловая скорость и момент инерции цилиндра относительно оси симметрии, проходящей через его центр инерции,

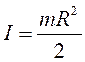;                                                      (3)