Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 2

Моменты инерции I_C  однородных тел правильной геометрической формы массой m относительно оси, проходящей через центр масс, определяются по формулам, указанным в таблице.

Формулы моментов инерции I_C однородных тел правильной геометрической формы массой m относительно оси, проходящей через центр масс

Если ось  не проходит через центр масс, то момент инерции тела относительно этой оси определяется по теореме Гюйгенса-Штейнера:

I_z = I_C + mb²,                                               (1.7)

где I_C – момент инерции тела относительно оси, параллельной оси  и проходящей через его центр масс;

b – расстояние между осями.

Простейшим случаем движения абсолютно твердого тела, ось вращения которого не закреплена, является плоское движение, т. е. движение, при котором все точки тела движутся параллельно одной заданной неподвижной плоскости. Примером плоского движения может служить качение симметричного (относительно оси вращения) тела (например, цилиндра).

Плоское движение абсолютно твердого тела можно разложить на два составляющих движения: поступательное и вращательное относительно мгновенной оси (например, относительно мгновенной оси, проходящей через центр масс тела). Угловая скорость вращательного движения не зависит от выбора точки, через которую проходит мгновенная ось вращения, и во всех случаях она имеет одинаковое значение. Скорость поступательного движения всех точек тела одинакова и равна скорости поступательного движения  его центра масс. Кинетическая энергия движущегося поступательно со скоростью  тела массой  определяется по формуле (1.1). Кинетическая энергия абсолютно твердого тела (АТТ) складывается из кинетической энергии поступательного и вращательного движения относительно мгновенной оси:

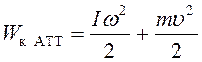,                                            (1.8)

где  – момент инерции тела относительно этой оси.

Механическая энергия системы равна сумме ее кинетической и потенциальной энергий: .

Потенциальная энергия тела характеризует его взаимодействие с  другими телами и полями, она зависит от взаимного положения тел и их положения во внешнем поле [3]. В частности, в поле силы тяжести Земли, вблизи поверхности Земли потенциальная энергия тела массой , центр тяжести которого находится на высоте  от некоторого произвольно выбранного начала отсчета, рассчитывается по уравнению

                                                  (1.9)

при условии, что у поверхности Земли потенциальная энергия тела принимается равной нулю, и зависимость ускорения свободно падающего тела  вблизи поверхности Земли от высоты не учитывается.

Потенциальная энергия упруго деформированного вдоль некоторой оси OX  тела жесткостью k (в поле силы упругости при малой линейной деформации)

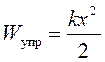                                                  (1.10)

при условии, что в недеформированном состоянии потенциальная энергия тела принимается равной нулю.

В общем случае работа , совершаемая силой  при перемещении материальной точки из точки M₁ в точку M₂, определяется по формуле:

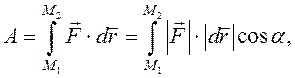                                   (1.11)

где  – скалярное произведение векторов силы  и перемещения ;

 – угол между этими векторами.

Из формулы (1.11) получаем выражение для работы, которая совершается силой, не зависящей от положения материальной точки:

.                                      (1.12)