Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 9

Дано: m1 = 20 г m2 = 2 кг v1 = 100 м/с	СИ 0,02 кг
, η - ?

Решение.

 

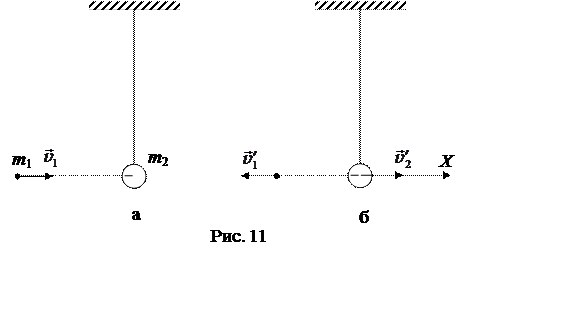Выберем начало отсчета потенциальной энергии системы в поле тяжес-ти Земли на высоте, на которой находятся пуля и центр шара в момент удара. Тогда до удара (рис. 11, а) и сразу после него (рис. 11, б) потенциальная энергия равна нулю.

В течение кратковременного взаимодействия при ударе на шар действуют силы тяжести и натяжения нити, которые уравновешивают друг друга. Сила взаимодействия пули с шаром является внутренней и не меняет полный импульс системы. Если пренебречь силой тяжести, действующей на пулю, малой по сравнению с силой взаимодействия, то можно считать, что результирующая сила, действующая на систему, равна нулю. Следовательно, выполняется закон сохранения импульса:

,                                                 (1)

где ,  – импульсы системы до и после удара.

При абсолютно упругом ударе (согласно его определению) диссипации механической энергии не происходит и наряду с законом сохранения импульса при ударе сохраняется механическая энергия:

.                                              (2)

где ,  – механическая энергия системы до и после удара.

Так как до удара шар покоился, импульс и механическая энергия системы равны импульсу и кинетической энергии пули соответственно:

;                                                   (3)

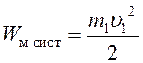.                                                (4)

Импульс и механическая энергия системы после удара рассчитываются по формулам:

;                                            (5)

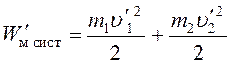.                                       (6)

После подстановки формул (3) и (5) в уравнение (1) оно примет вид:

.                                            (7)

Запишем равенство (7) в проекциях. Будем рассматривать движение пули и шара относительно системы отсчета, в которой ось  (рис. 11). Столкновение тел лобовое, поэтому ненулевыми будут проекции скорости тел только на ось ОХ:

.                                            (8)

Следовательно,

;                                                    (9)

          .                                                 (10)

Преобразовав формулу (7) с учетом выражений (4), (6), (9) и (10), получим:

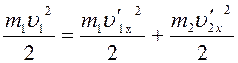.                                      (11)

Решение системы уравнений (8), (11) имеет вид [2, 3, 5]:

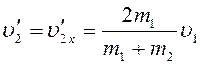.                                            (12)

С учетом равенства (11) выражение для импульса шара после удара примет вид:

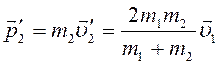.                                          (13)

Таким образом, направление импульса  совпадает с направлением скорости .

Для расчета значения модуля импульса используем данные задачи: 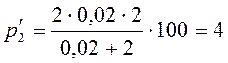 кг·м/с.

Энергия, которую передает пуля шару, равна кинетической энергии шара после удара: 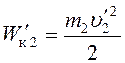. Энергия пули до удара описывается формулой (4). Доля энергии, которую пуля передает шару,

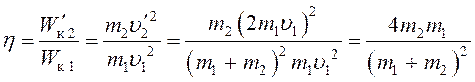.                (14)

Подставим данные задачи в формулу (14):

.

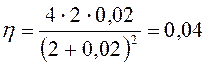Ответ: 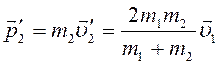,   ,    кг·м/с;

,   .

2.3. Закон сохранения момента импульса

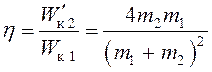Задача 10. На скамейке Жуковского (вращающемся диске) стоит человек и держит в руках тонкий стержень, расположенный горизонтально, так, что ось симметрии диска проходит  через середину стержня.  Скамейка вращается вокруг

своей оси симметрии, делая 5 об/с. Суммарный момент инерции человека и скамейки – 5 кг·м², масса стержня – 3 кг, его длина – 2 м. С какой частотой станет вращаться скамейка, если человек повернет стержень и расположит его вертикально вдоль оси симметрии скамейки? Какая работа будет совершена при этом? Трением пренебречь.

Дано: n = 5 об/с I1 = 5 кг·м2 m2 = 3 кг l = 2 м

n´, Ачел - ?

Решение.

Так как ось вращения системы «человек – скамейка – стержень» закреплена, будем рассматривать движение относительно системы отсчета, ось  которой совпадает с осью вращения системы и направлена вертикально вверх (рис. 12).