Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 5

 – скорость поступательного движения цилиндра, равная скорости его центра инерции относительно плоскости;

 – радиус цилиндра.

По условию задачи потерями механической энергии при качении ци-линдра можно пренебречь, поэтому механическая энергия цилиндра в начальном состоянии и у основания наклонной плоскости одинакова:

                                                     (4)

Так как скатывание цилиндра происходит без скольжения, скорость точек касания цилиндра относительно плоскости равна нулю: , а все другие точки цилиндра поворачиваются  вокруг мгновенной оси,  проходящей через по-

коящуюся точку касания. По закону сложения скоростей скорость точки касания равна сумме двух противоположно направленных слагаемых: скорости поступательного движения вместе с центром инерции и скорости движения по окружности при вращении вокруг оси, проходящей через центр инерции:  отсюда  Линейная скорость точки при вращательном движении абсолютно твердого тела (в рассматриваемом случае – цилиндра) связана с угловой скоростью соотношением:  Следовательно, модуль угловой скорости выражается через модуль скорости  и радиус цилиндра R:

.                                                    (5)

Направление угловой скорости  (от «нас») определяется по правилу буравчика в соответствии с направлением вращения цилиндра, показанным на рис. 3.

После подстановки соотношений (1) – (3), (5) в равенство (4) получим:

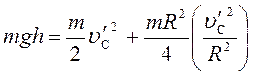.                                       (6)

Отсюда

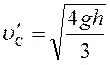.                                                          (7)

Подставив в формулу (7) численные значения, получим:  м/с.

Ответ: 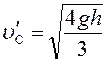,  м/с.

2.2. Закон сохранения импульса

Задача 4. Снаряд массой 12 кг, выпущенный из пушки под некоторым углом к горизонту, в верхней точке траектории имел скорость 30 м/с и разорвался на два осколка. Первый осколок массой 10 кг полетел в направлении движения снаряда со скоростью 40 м/с. Найти скорость второго осколка.

Дано: m = 12 кг m1 = 10 кг  = 30 м/с  = 40 м/с

- ?

Решение.

Внутренние силы, действующие на снаряд и осколки в момент взрыва, значительно больше внешних сил – тяжести и сопротивления воздуха, поэтому силами тяжести и сопротивления воздуха в момент взрыва можно пренебречь и считать систему замкнутой. Следовательно, к системе можно применить закон сохранения импульса:

,                                                 (1)

где  - импульс снаряда до его разрыва,

                                                 (2)

 импульс системы после разрыва снаряда,

;                                            (3)

  – скорость первого и второго осколков после разрыва снаряда.

Выберем для расчетов инерциальную систему отсчета, связанную с Землей. Мгновенная скорость материальной точки направлена по касательной к траектории в любой точке траектории. В частности, скорость снаряда в верхней точке его траектории направлена горизонтально, поэтому удобно направить горизонтальную ось  в сторону движения снаряда непосредственно перед его разрывом. Схематически состояние системы до разрыва снаряда показано на рис. 4, а, после него – на рис. 4, б. Отметим, что направление скорости второго осколка заранее не известно, оно определяется в результате решения задачи и может быть указано на рисунке только после решения.

 

Подставив формулы (2) и (3) в выражение (1), получим:

.                                                (4)

Выразим из формулы (4) скорость второго осколка после разрыва снаряда:

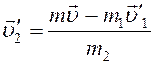;                                               (5)

Проекции скорости  на координатные оси имеют вид:

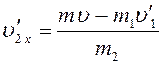;                                              (6)

.                                                (7)

Определим модуль скорости второго осколка после разрыва снаряда с учетом выражений (6) и (7):

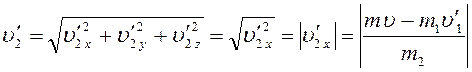.                   (8)

Подставим в уравнения (6), (8) численные значения, и получим:

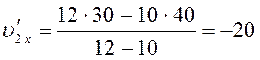м/с; 

 м/с.

Отрицательное значение проекции означает, что скорость второго осколка направлена в сторону, противоположную направлению оси .

Ответ: 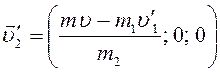;  м/с; .