![]() .
(3)
.
(3)
Подставив проекции импульса системы до выстрела (формула (1)) и после него (формула (2)) в равенство (3), получим:
![]() .
(4)
.
(4)
Отсюда
![]() .
(5)
.
(5)
Следовательно,
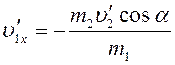 .
(6)
.
(6)
Модуль скорости отката орудия после вылета снаряда
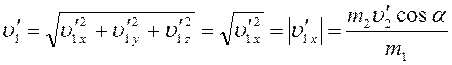 ,
(7)
,
(7)
так
как проекции скорости орудия на оси ![]() и
и ![]() равны
нулю.
равны
нулю.
Подставив
в уравнение (7) данные задачи, получим: ![]() м/с.
м/с.
При
откате на орудие действует постоянная сила трения, поэтому оно движется равнозамедленно.
Пусть ![]() – перемещение орудия до остановки (см. рис.
7). Для определения расстояния
– перемещение орудия до остановки (см. рис.
7). Для определения расстояния ![]() , пройденного орудием до
остановки, воспользуемся теоремой об изменении кинетической энергии:
, пройденного орудием до
остановки, воспользуемся теоремой об изменении кинетической энергии:
![]() ,
(8)
,
(8)
где
работы сил тяжести ![]() реакции опоры
реакции опоры ![]() и трения
и трения ![]() определяются
по выражениям:
определяются
по выражениям:
![]() (9)
(9)
![]() (10)
(10)
![]() (11)
(11)
а начальная кинетическая энергия – по формуле:
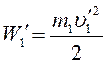 . (12)
. (12)
В
момент остановки скорость орудия ![]() и его кинетическая
энергия
и его кинетическая
энергия ![]() орудия равны нулю:
орудия равны нулю:
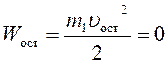 .
(13)
.
(13)
Таким образом, кинетическая энергия орудия полностью расходуется на преодоление силы трения.
После подстановки выражений (9) – (13) в соотношение (8) оно примет вид:
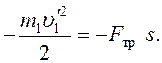 (14)
(14)
Отсюда
с учетом соотношения (6) найдем расстояние ![]() :
:
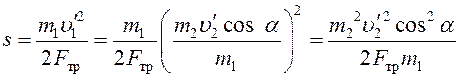 . (15)
. (15)
Подставляем в уравнение (15) данные задачи:
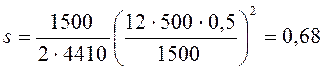 м.
м.
Ответ:
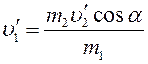 ,
, ![]() м/с;
м/с; 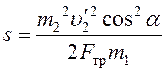 ,
, ![]() м.
м.
Задача 7. Из неподвижного орудия вылетает снаряд под углом 60° к горизонту со скоростью 200 м/с относительно орудия. Определить модуль ско-рости отката орудия относительно Земли сразу после вылета снаряда. Масса орудия равна 1520 кг, масса снаряда - 80 кг.
|
Дано:
|
|
|
|
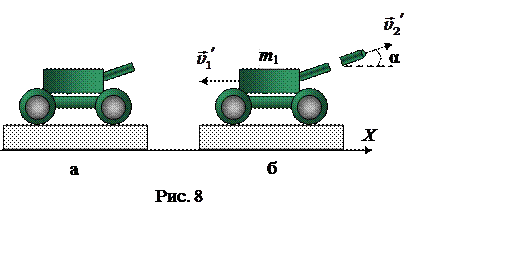
Рассмотрим изменение состояния системы «орудие – снаряд» относительно инерциальной системы отсчета, связанной с Землей. До вылета снаряда (рис. 8, а) импульс системы равен нулю:
![]() .
(1)
.
(1)
При
вылете снаряда из орудия происходит взаимодействие снаряда и орудия, в
результате которого орудие приобретает скорость ![]() относительно
Земли. Импульс системы после вылета снаряда (рис. 8, б)
относительно
Земли. Импульс системы после вылета снаряда (рис. 8, б)
![]() , (2)
, (2)
где
![]() – скорость снаряда относительно Земли.
– скорость снаряда относительно Земли.
По закону сложения скоростей
![]() .
(3)
.
(3)
Подставив соотношение (3) в правую часть формулы (2), получим:
![]() (4)
(4)
Силы
взаимодействия между снарядом и орудием являются внутренними, поэтому полный
импульс системы они изменить не могут. На систему действуют внешние силы:
реакции опоры, трения и тяжести. Время выстрела очень мало, поэтому действием
сил тяжести и трения на орудие во время вылета снаряда можно пренебречь Силой нормальной
реакции опоры, направленной вертикально, пренебречь
нельзя: она препятствует вертикальному движению орудия. Проекция импульса
системы на вертикальное направление в течение выстрела изменяется, так
как часть импульса орудия передается Земле, поэтому систему нельзя считать
замкнутой. Однако можно считать, что проекция результирующей внешней силы на
ось ![]() (см. рис. 8) равна нулю,
и, следовательно, проекция импульса системы на горизонтальное направление остается
постоянной:
(см. рис. 8) равна нулю,
и, следовательно, проекция импульса системы на горизонтальное направление остается
постоянной:
![]() .
(5)
.
(5)
Подставив проекции импульса системы до (формула (1)) и после (формула (4)) выстрела в равенство (5), получим:
![]() . (6)
. (6)
Отсюда
![]() . (7)
. (7)
Следовательно,
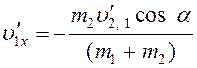 .
(8)
.
(8)
Модуль скорости отката орудия после вылета снаряда
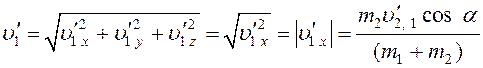 , (9)
, (9)
так
как проекции скорости орудия на оси ![]() и
и ![]() равны нулю.
равны нулю.
Подставив в уравнение (9) данные задачи, получим: 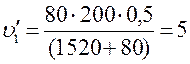 м/с.
м/с.
Ответ:
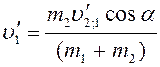 ,
, ![]() м/с.
м/с.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.