Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 6

Задача 5. Из ствола автоматического пистолета вылетела пуля массой 15 г со скоростью 28 м/с относительно Земли. Затвор массой 210 г прижимается к стволу невесомой пружиной жесткостью 220 кН/м. На какое расстояние от первоначального положения отойдет затвор после выстрела? Считать, что пистолет жестко закреплен. Трением между всеми телами пренебречь.

Дано: mп = 15 г mз = 210 г k= 220 кН/м  = 28 м/с	СИ 0,15 кг 0,21 кг 220∙103 Н/м
x - ?

Решение.

Движение затвора и пули является поступательным, следовательно, и затвор, и пулю можно считать материальными точками, масса которых сконцентрирована в их центрах инерции.

До выстрела (рис. 5, а) импульс системы «затвор – пуля»

,                                                     (1)

после выстрела (рис. 5, б) –

,                                           (2)

где ,  – скорость пули и затвора после выстрела соответственно.

          

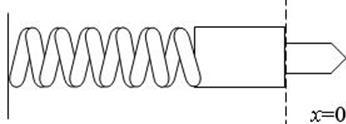
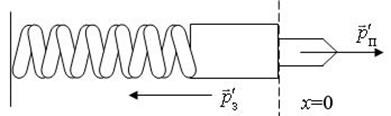
а                                                                   б

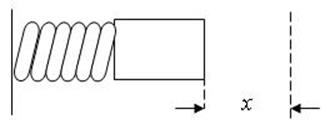
в

Рис. 5

При выстреле все внешние силы, действующие на систему, много меньше силы взаимодействия затвора и пули, поэтому выполняется закон сохранения импульса:

.                                                             (3)

Подставив формулы (1) и (2) в выражение (3), получим:

.                                                (4)

Следовательно, скорость затвора после выстрела

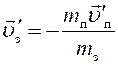.                                                 (5)

Отсюда модуль скорости затвора

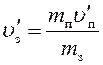.                                                   (6)

Так как пружина не деформирована, потенциальная энергия затвора в поле упругости пружины равна нулю, поэтому его механическая энергия сразу после выстрела равна кинетической:

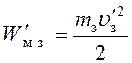.                                                  (7)

Затвор перемещается до остановки в направлении, противоположном направлению движения пули. В момент остановки (рис. 5, в) кинетическая энергия затвора равна нулю, а его механическая энергия - потенциальной:

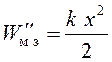.                                                   (8)

Так как по условию задачи трением можно пренебречь, при движении затвора выполняется закон сохранения механической энергии:

                                                  (9)

Подставив в уравнение (9) равенства (7) и (8), получим выражение:

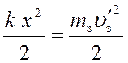,                                                   (10)

из которого с учетом формулы (6) найдем расстояние :

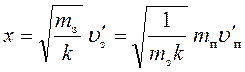.                                     (11)

Подставляем в формулу (11) данные задачи:  м.

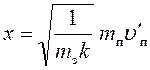Ответ: ;  м.

Задача 6. Из неподвижного орудия вылетает снаряд под углом 60° к горизонту со скоростью 500 м/с относительно Земли. Определить модуль ско-рости отката орудия сразу после вылета снаряда и расстояние, на которое орудие откатится, если сила трения, действующая на него при откате, равна 4410 Н. Масса орудия равна 1500 кг, снаряда – 12 кг.

Дано: кг кг Н °  м/с

s - ?

m2

Решение.

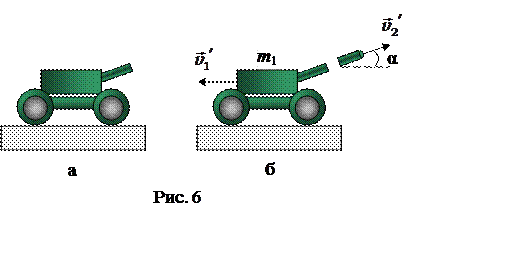
Рассмотрим изменение состояния системы «орудие – снаряд» относительно инерциальной системы отсчета, связанной с Землей. До вылета снаряда (рис. 6, а) импульс системы равен нулю:

.                                         (1)

Импульс системы после вылета снаряда (рис. 6, б)

.                                               (2)

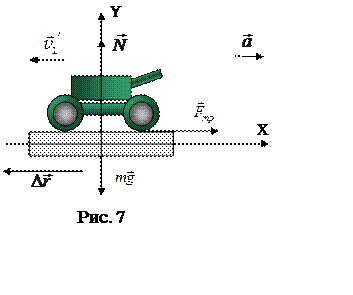Силы взаимодействия между снарядом и орудием являются внутренними, поэтому полный импульс системы они изменить не могут. На систему действуют внешние силы: реакции опоры, трения и тяжести. Время выстрела очень мало, поэтому действием сил тяжести и трения на орудие во время вылета снаряда можно пренебречь. Силой нормальной реакции опоры, направленной вертикально, пренебречь нельзя, она препятствует вертикальному движению орудия. Проекция импульса системы на вертикальное направление (рис. 7, ось ) в течение выстрела изменяется, так как часть импульса орудия передается Земле, поэтому систему нельзя считать замкнутой. Однако можно считать, что проекция результирующей внешней силы на ось  равна нулю, следовательно, проекция импульса системы на горизонтальное направление остается постоянной: