Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 12

Решение.

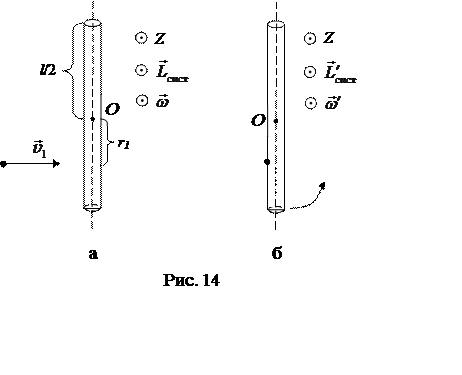
Будем рассматривать движение системы «стержень – пуля» относительно системы отсчета, начало которой расположено в центре стержня О, а ось  совпадает с осью вращения и направлена «на нас» (рис. 14). В момент удара на  систему действуют силы тяжести

и реакции опоры – оси. Линии действия сил реакции оси и тяжести, действующих на стержень, и силы тяжести, действующей на пулю, проходят через центр стержня О. Таким образом, все внешние силы являются центральными, их моменты относительно центра О равны нулю, следовательно, при столкновении выполняется закон сохранения момента импульса:

,                                                           (1)

где  и – моменты импульса системы относительно центра  непосредственно до удара (рис. 14, а) и сразу после него (рис. 14, б) соответственно[1].

До взаимодействия стержень был неподвижен, поэтому момент импульса системы равен моменту импульса пули:

,             (2)

где  – момент инерции пули относительно оси вращения;

 – угловая скорость пули непосредственно перед ударом.

Примем пулю за материальную точку, тогда ее момент инерции относительно оси вращения

.                                            (3)

Модуль угловой скорости пули выражается через модуль линейной скорости  и расстояние  от точки попадания пули до оси

,                                                        (4)

где

Направление  (рис. 14, а – «на нас») определяется по правилу буравчика в соответствии с направлением вращения.

После взаимодействия пули и стержня система начинает вращение как одно целое с угловой скоростью  поэтому

,                            (5)

где  – угловая скорость системы непосредственно после удара.

Момент инерции стержня относительно оси вращения, которая в рассматриваемом случае совпадает с осью симметрии стержня, определяется по формуле:

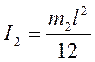.                                                     (6)

Подставив формулы (2) и (5) в уравнение (1), получим соотношение:

.                                               (7)

Отсюда

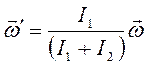.                                                 (8)

Заметим, что моменты импульса пули до и после удара можно вычислить, основываясь на определении момента импульса материальной точки:  и .

При анализе выражения (8) можно сделать два вывода:

1) угловая скорость системы во втором состоянии сонаправлена с угловой скоростью пули в первом состоянии: ;

2) так как моменты инерции величины положительные, модуль угловой скорости  определяется по формуле:

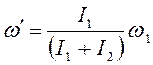.                                               (9)

Подставим выражения (3), (4) и (6) в равенство (9):

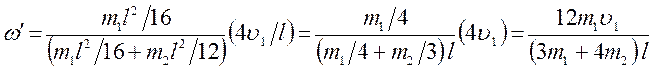.  (10)

Подставим данные задачи в уравнение (10) и получим:

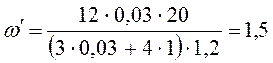 рад/с.

Ответ: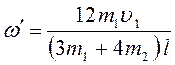,  рад/с.

Библиографический список

1. С а в е л ь е в  И. В. Курс общей физики: В 5 кн. Кн. 1. Механика / И. В. С а в е л ь е в. М., 1998. 336 с.

2. Я в о р с к и й  Б. М. Курс физики / Б. М.  Я в о р с к и й, А. А.  Д е т л а ф, Л. Б.  М и л к о в с к а я. М., 2001. 718 с.

3. Т р о ф и м о в а Т. И. Курс физики / Т. И.  Т р о ф и м о в а. М., 2004. 542 с.

4. Физический энциклопедический словарь / Под ред. А. М. Прохорова.  М., 1984. 940 с.

5. Д ж а н к о л и  Д. Физика / Д.  Д ж а н к о л и.  М., 1989. Т. 1. 667 с.

6. Н и к и т и н  Н. Н. Курс теоретической механики / Н. Н.  Н и к и т и н. М., 1990. 607 с.

_________________________________________________

Учебное издание

ДРОЗДОВА Илга Анатольевна,  ТОДЕР Георгий Борисович

ЗАКОНЫ  СОХРАНЕНИЯ  В  МЕХАНИКЕ

(ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ)

Редактор Т. С. Паршикова

***

Подписано в печать     . 02.2010. Формат 60 ´ 84 ¹/₁₆.

Плоская печать. Бумага офсетная. Усл. печ. л. 2,4. Уч.-изд. л. 2,6.

Тираж 800 экз.  Заказ         .

**

Редакционно-издательский отдел ОмГУПСа

Типография ОмГУПСа

*

644046, г. Омск, пр. Маркса, 35

 

И. А. ДРОЗДОВА,  Г. Б. ТОДЕР

ЗАКОНЫ  СОХРАНЕНИЯ  В  МЕХАНИКЕ

(ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ)

ОМСК  200

Рис.1

9