Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 11

Задача 11. Человек, стоящий на неподвижной скамейке Жуковского, держит вращающийся сплошной цилиндр, расположенный вертикально, так, что оси симметрии скамейки и цилиндра совпадают. Цилиндр вращается вокруг своей оси с угловой скоростью 16,5 с^-1. Суммарный момент инерции человека и скамейки – 7 кг·м², масса цилиндра – 7 кг, его радиус – 0,2 м. С какой угловой скоростью станет вращаться скамейка, если человек развернет цилиндр на 180° и расположит его вертикально так, чтобы оси симметрии скамейки и цилиндра совпали, модуль угловой скорости цилиндра относительно скамейки остался прежним, а ее направление изменилось на противоположное? Трением в оси пренебречь.

Решение:

Так как ось вращения системы «человек – скамей-ка – цилиндр» закреплена, будем рассматривать движение тел относительно системы отсчета, связанной с Землей, ось  которой совпадает с осью вращения системы и направлена вертикально вверх (рис. 13).

Моменты сил тяжести, действующих на все тела, входящие в систему, и силы реакции опоры, действующей на скамейку, в рассматриваемых положениях тел равны нулю,  так как линии действия  этих сил  совпадают  с осью враще-

ния системы (система симметрична относительно оси вращения), у сил нет плеч, поэтому они не могут изменять вращательное движение системы. Моментом силы трения при изменении положения цилиндра можно пренебречь. Таким образом, результирующий момент внешних сил можно считать равным нулю, поэтому для решения задачи можно применить закон сохранения момента импульса:

,                                                           (1)

где  и  – момент импульса системы при первом и втором положениях цилиндра соответственно.

Момент импульса системы равен векторной сумме моментов импульсов тел, входящих в систему, поэтому

;                                                    (2)

,                                     (3)

где  – момент инерции цилиндра относительно оси вращения;

 и  – угловые скорости тел относительно Земли в состоянии системы сразу после изменения положения цилиндра.

Так как при изменении положения цилиндр вращается не только вокруг своей оси, но и вместе со скамейкой, его угловая скорость относительно Земли

.                                                  (4)

Направления угловых скоростей  (рис. 13, а, вдоль оси вращения цилиндра вверх) и  (рис. 13, б, вдоль оси вращения цилиндра вниз) определяются по правилу буравчика в соответствии с направлением вращения цилиндра. Направление угловой скорости  заранее не известно (определяется при решении задачи), поэтому на рис. 13, б оно отмечено знаком вопроса.

Подставив формулы (2) - (4) в уравнение (1), после преобразований получим соотношение:

.                                       (5)

Отсюда выразим угловую скорость:

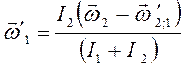.                                               (6)

Выражение (6) в проекции на ось  (см. рис. 13) принимает вид:

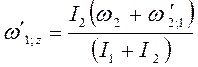.                                             (7)

Так как моменты инерции величины положительные, , поэтому

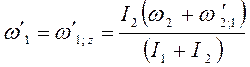                                       (8)

и , следовательно, и направление вращения скамейки в состоянии системы после изменения положения цилиндра совпадает с направлением вращения цилиндра в первом состоянии.

Момент инерции цилиндра относительно оси вращения, которая в рассматриваемом случае совпадает с его осью симметрии, определяется по формуле:

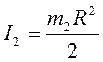.                                                     (9)

Подставив формулу (9) в выражение (8), получим:

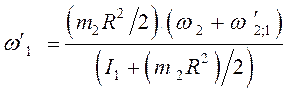,                                    (10)

Подставим данные задачи в формулу (10) и получим:  с^-1.

Ответ: 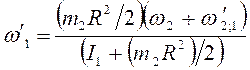,   ,    с^-1.

Задача 12. Вертикально расположенный деревянный стержень закреплен так, что может вращаться вокруг оси, проходящей через его середину. Пуля, летящая горизонтально со скоростью 20 м/с, попадает в стержень и застревает в нем на расстоянии, равном одной четвертой его длины, от оси вращения. С какой угловой скоростью станет вращаться стержень, если его масса равна 1кг, длина – 1,2 м, а масса пули – 30 г? Трением в оси пренебречь.