Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 3

При движении материальной точки в поле консервативных сил это поле совершает работу, не зависящую от пути, по которому движется точка. При перемещении материальной точки из положения, определяемого радиусом-векто-ром , в положение, определяемое радиусом-вектором , работа консервативной силы равна убыли потенциальной энергии точки:

.                                           (1.13)

Например,

;                                  (1.14)

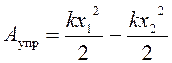.                                           (1.15)

При вращении абсолютно твердого тела вокруг неподвижной оси  внешняя сила, создающая момент  совершает работу:

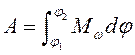,                                               (1.16)

где  – проекция вектора  на направление угловой скорости.

Знак работы зависит от знака

Связь между характеристиками движения и мерами действия силы отражается в общих теоремах динамики [4, 6] об изменении импульса, момента импульса и кинетической энергии. Из этих теорем выводятся законы сохранения импульса, момента импульса и механической энергии соответственно. Эти законы описывают свойства движения и взаимодействия любой системы материальных точек.

Теорема об изменении кинетической энергии: изменение кинетической энергии системы при ее переходе из состояния 1 в состояние 2 происходит под действием сил, приложенных к точкам системы, и равно сумме работ этих сил при данном переходе:

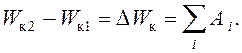                                  (1.17)

С помощью теоремы об изменении кинетической энергии решаются многие задачи механики.

Сила называется диссипативной, если ее действие приводит к диссипации механической энергии – переходу механической энергии в тепловую. Все силы сопротивления движению (например, сила трения) являются диссипативными.

Закон сохранения механической энергии: при отсутствии диссипативных сил механическая энергия системы остается постоянной, она может переходить из кинетической энергии в потенциальную и обратно:

                                            (1.18)

Сила называется консервативной, если ее работа по изменению состояния системы зависит только от начального и конечного состояния системы и не зависит от способа изменения состояния. Консервативные силы не являются диссипативными, поэтому закон сохранения механической энергии выполняется, если на систему и внутри нее действуют только консервативные силы.

При наличии диссипативных сил к системе применим общефизический закон сохранения энергии: энергия в природе ниоткуда не возникает, никуда не исчезает, а при любых взаимодействиях лишь переходит из одной формы в другую, от одного тела к другому.

Закон сохранения импульса: если результирующая внешних сил, действующих на систему, равна нулю, то полный импульс системы не меняется при любых взаимодействиях внутри системы:

                                              (1.19)

Система называется замкнутой, если на нее не действуют внешние силы, поэтому в замкнутых системах закон сохранения импульса выполняется.

В случае, когда результирующая внешних сил не равна нулю, но ее проекция на некоторое направление обращается в нуль, остается постоянной проекция импульса системы на это направление.

Закон сохранения момента импульса: если результирующий момент внешних сил, действующих на систему, равен нулю, то полный момент импульса системы не меняется при любых взаимодействиях внутри системы:

                                             (1.20)

Силы, направленные только к одной точке или от нее, называются цент-ральными, а эта точка – центром. Момент центральной силы равен нулю, поэтому для систем, на которые действуют только центральные силы, также как и для замкнутых систем, справедлив закон сохранения момента импульса.

В случае, когда результирующий момент внешних сил, действующих на систему, не равен нулю, но его проекция на некоторую ось (момент сил относительно оси) равна нулю, момент импульса системы относительно этой оси остается постоянным.