 Моменты сил тя-жести,
действующих на все тела, входящие в систему, и силы реакции опоры,
действующей на скамейку, в рассматриваемых положениях тел равны нулю, так как
линии действия этих сил совпадают с осью вращения системы (система симметрична
относительно оси вращения), у сил нет плеч, поэтому они не могут изменять вращательного движения системы. Силой
трения между осью и вращающимся диском при кратковременном изменении положения
стержня можно пренебречь. Таким образом, результирующий момент внешних
сил можно считать равным нулю и для решения задачи можно применять закон
сохранения момента импульса:
Моменты сил тя-жести,
действующих на все тела, входящие в систему, и силы реакции опоры,
действующей на скамейку, в рассматриваемых положениях тел равны нулю, так как
линии действия этих сил совпадают с осью вращения системы (система симметрична
относительно оси вращения), у сил нет плеч, поэтому они не могут изменять вращательного движения системы. Силой
трения между осью и вращающимся диском при кратковременном изменении положения
стержня можно пренебречь. Таким образом, результирующий момент внешних
сил можно считать равным нулю и для решения задачи можно применять закон
сохранения момента импульса:
![]() ,
(1)
,
(1)
где
![]() и
и ![]() – моменты
импульса системы при горизонтальном и вертикальном положениях стержня
соответственно.
– моменты
импульса системы при горизонтальном и вертикальном положениях стержня
соответственно.
Момент импульса системы равен векторной сумме моментов импульсов тел, входящих в систему, поэтому
![]() ;
(2)
;
(2)
![]() ,
(3)
,
(3)
где
![]() и
и ![]() –
моменты инерции стержня относительно оси вращения при его горизонтальном и
вертикальном положениях;
–
моменты инерции стержня относительно оси вращения при его горизонтальном и
вертикальном положениях;
![]() и
и ![]() – угловые скорости системы в соответствующих
состояниях.
– угловые скорости системы в соответствующих
состояниях.
Направление
угловой скорости ![]() (рис. 12, а) вдоль оси вращения
вверх определяется по правилу буравчика в соответствии с направлением вращения
системы. Направление угловой скорости
(рис. 12, а) вдоль оси вращения
вверх определяется по правилу буравчика в соответствии с направлением вращения
системы. Направление угловой скорости ![]() заранее
не известно (определяется при решении задачи), поэтому на рис. 12, б оно отмечено
знаком вопроса.
заранее
не известно (определяется при решении задачи), поэтому на рис. 12, б оно отмечено
знаком вопроса.
Подставив формулы (2) и (3) в уравнение (1), получим соотношение:
![]() (4)
(4)
Отсюда выразим угловую скорость:
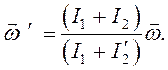 (5)
(5)
Выражение (5) позволяет сделать два вывода:
1)
угловая скорость системы при вертикальном положении стержня со-направлена с
угловой скоростью системы при его горизонтальном положении: ![]() , следовательно, и направление вращения
системы не меняется;
, следовательно, и направление вращения
системы не меняется;
2) так как моменты инерции величины положительные, модуль угловой скорости системы при вертикальном положении стержня определяется по формуле:
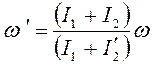 .
(6)
.
(6)
Связь
модулей угловых скоростей ![]() и
и ![]() с соответствующими частотами вращения
с соответствующими частотами вращения ![]() и
и ![]() описываются
уравнениями:
описываются
уравнениями:
![]() (7)
(7)
![]() (8)
(8)
Стержень считается тонким и при вертикальном положении совпадает с осью вращения, поэтому его момент инерции относительно оси вращения можно принять равным нулю:
![]() .
(9)
.
(9)
При горизонтальном положении стержня его момент инерции относительно оси вращения, которая в рассматриваемом случае совпадает с осью симметрии стержня, определяется по формуле:
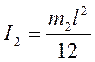 . (10)
. (10)
Подставив
формулы (7) – (10) в выражение (6) и сократив обе части полученного соотношения
на ![]() получим формулу для определения частоты
вращения системы:
получим формулу для определения частоты
вращения системы:
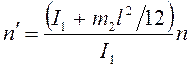 .
(11)
.
(11)
Подставив
данные задачи в уравнение (11), получим: ![]() об/с.
об/с.
Для определения работы, совершаемой человеком при изменении положения стержня, применим теорему об изменении кинетической энергии:
![]() ,
(12)
,
(12)
где
![]() ,
, ![]() – кинетическая
энергия системы при горизонтальном и вертикальном положениях стержня соответственно,
– кинетическая
энергия системы при горизонтальном и вертикальном положениях стержня соответственно,
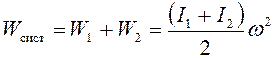 ; (13)
; (13)
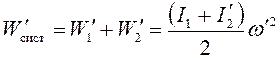 .
(14)
.
(14)
Работы
сил реакции опоры ![]() , тяжести
, тяжести ![]() ,
приложенных к каждому телу, равна нулю, так как моменты этих сил относительно
оси вращения равны нулю, работа сил трения в оси
,
приложенных к каждому телу, равна нулю, так как моменты этих сил относительно
оси вращения равны нулю, работа сил трения в оси ![]() пренебрежимо
мала по условию, поэтому
пренебрежимо
мала по условию, поэтому
![]() .
(15)
.
(15)
Подставив выражения (13) – (15) в равенство (12) и выполнив преобразования полученной формулы с учетом уравнений (6) – (10), получим формулу для определения работы, совершаемой человеком:
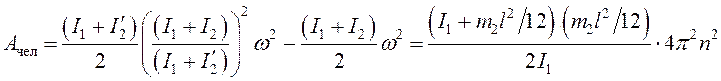 . (16)
. (16)
Подставив
численные значения в формулу (16), получим: ![]() Дж.
Дж.
Ответ:
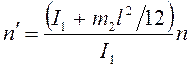 ,
, ![]() об/с;
об/с;
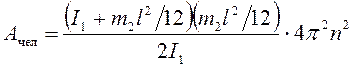 ,
, ![]() Дж.
Дж.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.