Законы сохранения в механике (примеры решения задач): Методические указания к решению задач по физике, страница 8

Задача 8. Два маленьких шара подвешены на нитях одинаковой длины так, что поверхности шаров соприкасаются. Расстояние от точек подвеса до центров масс шаров одинаково и равно 0,3 м. Масса первого шара – 400, второго – 200 г. Нить, на которой подвешен первый шар, отклоняют на некоторый угол и отпускают. Найти этот угол, если известно, что при абсолютно неупругом ударе шаров выделилась тепловая энергия 98 мДж. Радиусы шаров считать много меньшими длины нитей.

Решение.

Так как расстояние от точки подвеса до цент-ра масс каждого шара много больше радиусов шаров, шары можно считать материальными точками, массы которых сконцентрированы в центрах масс шаров. Будем отсчитывать высоту и потенциальную энергию в поле тяжести от уровня, на котором расположены центры масс шаров, вертикально висящих на нитях и находящихся в равновесии.

Рассматриваемые при решении состояния системы шаров изображены на рис. 9. Начальному состоянию, представленному на рис. 9, а, соответствует положение первого (левого) шара массой  на высоте  при отклонении держащей его нити на угол . Второй (правый) шар массой  покоится в положении равновесия на вертикально висящей нити. Скорость, а значит, и кинетическая энергия шаров, равна нулю, следовательно, полная механическая энергия системы равна потенциальной энергии первого шара.

Непосредственно перед ударом (рис. 9, б) потенциальная энергия шаров равна нулю. Первый шар движется со скоростью , второй – покоится. Следовательно, механическая энергия системы до удара равна кинетической энергии первого шара:

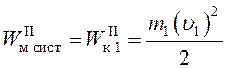,                                           (1)

а импульс системы равен импульсу первого шара:

.                                                  (2)

.                                             (3)

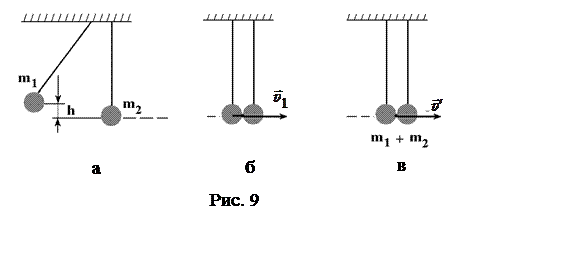
Сразу после удара (рис. 9, в) шары движутся как одно целое со скоростью  (по условию задачи удар абсолютно неупругий), поэтому импульс системы равен векторной сумме импульсов обоих шаров:

.                                   (4)

Потенциальная энергия шаров остается равной нулю, поэтому механи-ческая энергия системы равна кинетической энергии шаров:

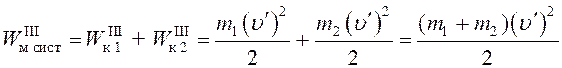.             (5)

При переходе системы из первого состояния во второе (при падении первого шара в поле силы тяжести Земли) сила натяжения нити работы не совершает, так как  в любой момент времени  движения она перпендикулярна перемещению,

а диссипативные силы трения и сопротивления воздуха пренебрежимо малы, поэтому полная механическая энергия шара остается постоянной:

.                                               (6)

При движении шара его потенциальная энергия убывает и переходит в кинетическую. Подставим правые части равенств (1) и (2) в формулу (6):

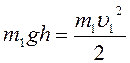.                                                (7)

При переходе системы из второго состояния в третье (при абсолютно неупругом ударе) в течение кратковременного взаимодействия шаров на них действуют внешние силы: тяжести и натяжения нитей. Векторная сумма этих сил равна нулю, поэтому выполняются закон сохранения импульса:

                                                  (8)

и закон сохранения энергии (часть механической энергии системы переходит в тепловую ):

.                                           (9)

С учетом равенств (3) и (4) формула закона сохранения импульса (8) примет вид:

.                                         (10)

Векторы в левой и правой частях формулы (10) равны, поэтому равны и их модули:

.                              (11)

С учетом выражений (2) и (5) уравнение (9) примет вид:

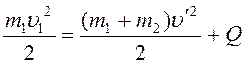.                        (12)

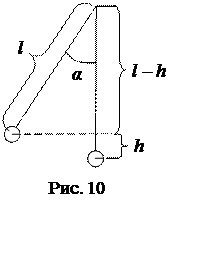
Из рис. 10 видно, что , отсюда

.                                (13)

Решая совместно уравнения (7), (11) - (13), найдем угол :

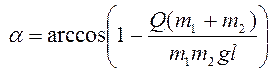.                                      (14)

Подставив в уравнение (14) данные задачи, получим: °.

Ответ: ; °.

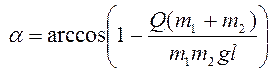Задача 9. Пуля массой 20 г летит горизонтально со скоростью 100 м/с и сталкивается с шаром массой 2 кг, подвешенным на нити. Найти импульс шара после удара и долю энергии пули, переданной шару при ударе, если удар лобовой и абсолютно упругий.