Теоретические и экспериментальные исследования закономерностей измельчения топлива, страница 8

Следует также отметить, что иногда при рассмотрении измельчения идеальных тел применяют закон Риттингера в виде (2.11). Однако при этом [95, 120] вместо величины i_s используют кратность измельчения, определенную по размерам максимальных кусков, – i_max. Как уже отмечалось ранее, достоверность определения на практике максимальных размеров кусков (D_max и d_max) достаточно низка, а сама характеристика i_max весьма противоречива.

Оригинальность предлагаемого в данной работе подхода при исследовании закономерностей размола полидисперсного топлива в мельницах заключается в использовании закона Риттингера в строгом соответствии с его определением в виде (2.11), т. е. с учетом средних размеров кусков до D_s и после d_s измельчения, а также определенной по этим показателям величины кратности измельчения i_s.

2.4.1 Теория идеального измельчения

Рассмотрим гипотезу Риттингера (2.8) на примере идеального разрушения тела правильной формы, например, кубика с размером ребра D.

В результате идеального разрушения можно получить n_d новых кубиков с размером ребра d.

Поверхность тела до и после измельчения равна соответственно S_D = 6D² и S_d = n_d×6d².

Приращение вновь образованной поверхности DS составит

.                          (2.15)

Учитывая, что суммарный объем вновь полученных кубиков равен объему исходного тела, можно записать

,                                      откуда следует, что

.                                                   

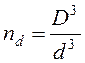Тогда (2.15) можно переписать как

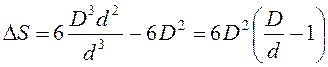                                или с учетом, что кратность измельчения равна i = D / d, как

.                                     (2.16)

Подстановка (2.16) в (2.8) показывает, что затраты энергии Е, Дж, при измельчении кусочка на равновеликие части по закону Риттингера равны

,                                    (2.17)

где k_S – коэффициент пропорциональности, Дж/м².

Приращение поверхности DS, отнесенное к объему V_D измельчаемого тела, можно записать как

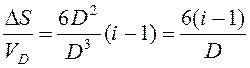.                             (2.18)

Приращение поверхности DS, отнесенное к единице массы измельчаемого тела, можно записать как

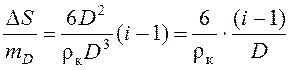.                         (2.19)

где m_D – масса измельчаемого тела, кг, m_D = r_кV_D = r_к D³; r_к – кажущаяся плотность измельчаемого материала, кг/м³.

В технике измельчения затраты энергии на размол принято относить к единице массы измельчаемого материала.

Тогда, согласно гипотезе Риттингера (2.8) с учетом (2.19) для удельной энергии, затраченной на измельчение, Э, Дж/кг, можно записать

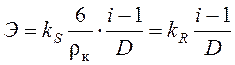,                              (2.20)

что по форме соответствует уравнению (2.11), полученному путем интегрирования общего выражения (2.10), объединяющего законы измельчения.

Если, рассматривая идеальное разрушение, кубическую форму измельчаемого куска поменять на шар диаметром D, то результирующее выражение (2.20) не изменится, т. к. удельная поверхность, отнесенная к объему (или массе), для шара и куба одинакова, что видно из следующего:

шар

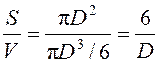;                                              куб

.                                               

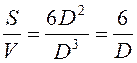Если ввести в рассмотрение в качестве исходных n_D частиц размером D, то итоговое выражение для удельной энергии (2.20) не изменится.

В случае полидисперсного материала совокупность частиц до и после размола можно осреднить (по массе) частицами с соответствующими размерами D_s и d_s. Рассматривая далее идеальное измельчение полидисперсного материала, итоговое выражение для удельной энергии (2.20) формально также не изменится (за исключением нижних индексов s при величинах i и D).

Размол влажного полидисперсного материала в мельнице совмещен с подсушкой топлива, т. е. процесс протекает с изменением начальной массы материала (плотности вещества), но при сохранении его первоначального объема. Однако и в этом случае, рассматривая идеальное измельчение влажного полидисперсного материала с изменением в результате сушки его массы, итоговое выражение для удельной энергии (2.20) также не изменится, т. к. энергозатраты и приращение поверхности отнесены к 1 кг сырого топлива.