Проектирование поперечного профиля автомобильных дорог с учетом движения потоков автомобилей. Проектирование плана и продольного профи­ля с учетом движения потоков автомобилей, страница 3

Аналогичная формула была предложена М. Ф. Смирновым:

где А — коэффициент размерности; ψ_c — коэффициент снижения пропускной способности.

Проведенный Л. А. Кероглу [31] анализ этих двух уравнений показал, что полученные результаты имеют существенные разли­чия. Так, по формуле Д. А. Вулиса при трех полосах движения пропускная способность равна 1240—1730 авт/ч, а по формуле М. Ф. Смирнова — 1000 авт/ч. Такое расхождение, видимо, объяс­няется различием коэффициентов снижения пропускной способ­ности.

При использовании макроскопических моделей движения тран­спортных потоков пропускная способность определяется на осно­ве уравнений движения и неразрывности. Из общего уравнения неразрывности (1У.27) получают уравнение для определения ско­рости движения в зависимости от плотности

Отсюда уравнение «интенсивность—плотность» будет иметь вид

Дифференцируя уравнение (V11.5) по плотности q и приравни­вая его нулю, получаем величину оптимальной плотности, соот­ветствующей пропускной способности:

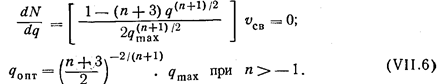
Величину скорости, соответствующую оптимальной плотности, получают путем подстановки величины q_опт в уравнение (УП.4);

Отсюда величина пропускной способности (максимальной ин­тенсивности движения)

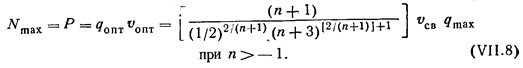
Преимущество применения макроскопических теорий заклю­чается в возможности оценки пропускной способности не только одной полосы, но и большого числа полос на автомагистралях, имеющих разделительные полосы.

Пропускная способность может быть также определена на ос­нове уравнения следования за лидером. Рассмотрим уравнение, в котором степень при расстоянии между автомобилями равна 2:

С учетом предположения, что все автомобили движутся в со­ответствии с уравнением (УП.9), можно записать

Умножая обе части на dt, получаем

Интегрируя, получаем

где С — постоянная интегрирования.

Учитывая, что плотность q = 1/x, уравнение (VII.12) можно записать так:

Постоянные К и С могут быть определены на основе следую­щих граничных условий: 1) максимальная плотность q = q_max при v = 0; 2) максимальная скорость v = v_св  при q = 0.

Из второго условия получаем С = v_o; из первого условия

Подставляя значения К. и С в уравнение (VII. 13), находим

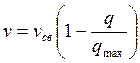,                (VII.14)

Используя зависимость N = qv, получаем зависимость «интен­сивность—плотность»

Отсюда пропускная способность, т. е. N_max, равна

При любых значениях показателя степени при расстоянии между автомобилями [см. уравнение (VII.9)] уравнение для рас­чета пропускной способности имеет вид

P = v_опт q_max e^-1,                   (VI1.17)

где Vопт — скорость, соответствующая пропускной способности; е — основание натуральных логарифмов.

По формуле (VII. 17) может быть определена пропускная спо­собность полосы движения.

В исследованиях часто применяют метод, основанный на ис­пользовании зависимостей «скорость — плотность», получаемых путем наблюдений. Точность оценки пропускной способности по этому методу определяется надежностью зависимости «скорость— плотность».

Исследование показывает, что на зави­симость «скорость — плотность» оказывают влияние состав дви­жения и дорожные условия. Для практических целей ее можно принять прямолинейной. Тогда уравнение для расчета пропускной способности будет иметь вид

Величина коэффициента α зависит от условий движения и мо­жет меняться в пределах от 0,19 до 0,25. А. Н. Красниковым для автомагистралей было получено значение α =0,23.

В табл. VII. 2 сопоставлены величины пропускной способности полосы движения, полученные разными методами.

Значения, наиболее близкие к фактическим, дают методы, ос­нованные на использовании гидродинамических теорий, теорий следования за лидером и упрощенных динамических моделей 3-й группы.

В качестве расчетной формулы можно рекомендовать уравне­ние VII. 18. Это уравнение имеет следующие преимущества: поз­воляет достаточно просто набирать статистические материалы по пропускной способности полосы движения в разных дорожных условиях (достаточно замерить v_св и q_max); дает результаты, хо­рошо согласуемые с результатами наблюдений; позволяет отка­заться от зависимостей «скорость — плотность», получение кото­рых связано со сложностью измерений и обработки.