Отсюда длина полосы ^п:г=^I^~!!• (VIII.22)
Оптимальная длина зоны разгона и перестроения (вливания) медленно движущихся автомобилей может быть установлена из условия минимума суммарных транспортных потерь вследствие задержки (определяемой по продолжительности задержки) автомобилей при вливаняи на этом участке и затрат на строительство полос.
Пусть в точке О (рис. VIII.8) происходит слияние двух потоков, движущихся по дополнительной и скоростной полосам. Поток быстрых автомобилей, движущихся по скоростной полосе, имеет скорость ио и плотность ^^, а поток медленно движущихся соответственно Ущ и <7м. Пусть задана длина уширения 1^. Предположим, что вливание медленно движущегося автомобиля происходит следующим образом: после точки О (вершина подъема) медленный автомобиль набирает скорость с ускорением а. Вливание
происходит в точке О, если быстрый автомобиль находится на большом расстоянии и не догонит медленный автомобиль, вышедший на скоростную полосу. Если медленный автомобиль не смог влиться на скоростную полосу на расстоянии /4, то он задерживается в точке /.
|
|
Минимальный интервал между быстро и медленно движущимися автомобилями, при котором быстрый не догонит медленный, движущийся с начальной скоростью Ув, равен (см. рис. VIII.8):
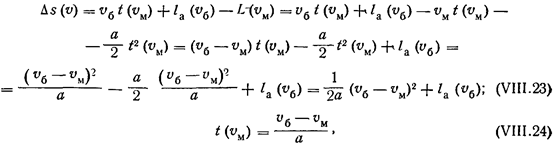
где Ц»и)—время от момента вливания медленно движущегося автомобиля, имеющего скорость v, до момента, когда он набирает скорость Об," ^(^м) — путь, пройденный медленно движущимся автомобилем от момента вливания до момента, когда он на'берет скорость Об; 1& ("в) — минимальное расстояние между автомобилями, движущимися со скоростью г>б (динамический габарит).
Для определения времени, затрачиваемого медленно движущимися автомобилями для вливания, предварительно определяем плотность этих автомобилей (]м(х), не перестроившихся до точки х (см. рис. УП1.8). Очевидно, что величина ^и(х) есть убывающая функция от х по формуле полной вероятности:
![]()
где Д — бесконечно малое приращение расстояния х; 1 — вероятность того, что на участке (х+Д; х+2А) имеется медленно движущийся автомобиль, не совершивший перестроения до точки х; 2 — вероятность того, что на участке (х, .х+Д) имеется медленно движущийся автомобиль, не совершивший перестроения до точки х; 3 — вероятность того, что на участке (х, х+Д) имеется быстро движущийся автомобиль; 4 — вероятность того, что интервал за быстро движущимся автомобилем недостаточен для совершения перестроения в точке х, т. е. интервал менее их; 5 — вероятность того, что на участке (х; х+Д) нет быстро движущегося автомобиля; 6—0(Д)—бесконечно малая высшего по рядка; 0(Д)=0
Раскрывая скобки (выражения VIII.25), получаем:
![]()
Переходя к пределу А—-0, получаем уравнение (УП1.26) в виде
![]()
Из 0/111.27) имеем
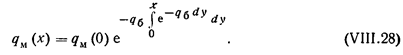
В точке /4 (см. рис. УП1.8) будем иметь плотность медленно ^кТ^" автомобилей' не совершивших перестроения Га уча
^(^^о6-'76^96"' (УП1.29) ЙстТо6 г,)6 ^доля медленн0 Я^У"™ автомобилей, не перестроившихся на
Отсюда, зная плотность медленно движущихся автомобилей Дви-жТи^^^^^^^^^^^^^^ /4 можн0 опртоть ———ивносТь
^-^(^м^). (уш.зо)
^б •°и (^) -- скорость медленно движущихся автомобилей в точке Ц- а (М-плот движ^я!"0 ^У™ ^омобилей в точке I , не влившихся в поток быстро
Зная величину интенсивности из уравнения (VIII 30) можно
"Т^ке ТТ^ Г^ в точке 1и ^Днее время ожидания В точке /4 (или х) мы имеем систему массового обслуживания
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.