z1 = N / P1; z2 = N / P2. (VIII.2)
Математическое ожидание числа автомобилей, находящихся на рассматриваемых элементах:
![]()
Вероятность отсутствия автомобилей на рассматриваемых элементах
![]()
Определение приведенных выше показателей для каждой системы элементов позволяет дать количественную оценку выбранного сочетания. Пересмотр выбранного сочетания элементов целесообразно осуществлять при v ≤ 0,3 и получении больших значений М(k); z1; z2 и малых Р(0,0). В среднем следует выбирать размеры соседних элементов такими, чтобы величины v были более 0,5, а коэффициент аварийности более 0,6.
VIII. 2. ОЦЕНКА УЧАСТКОВ ПОДЪЕМОВ ИЗ УСЛОВИЯ ДВИЖЕНИЯ ПОТОКОВ АВТОМОБИЛЕЙ
Основной особенностью движения потоков автомобилей на подъемах является резкое увеличение числа автомобилей, движущихся в очереди за медленно движущимся автомобилем вследствие отсутствия возможности совершить обгон. Величину продольного уклона, длину подъема и поперечный профиль дороги на этом участке необходимо устанавливать из условия возможности сокращения потерь времени и повышения скоростей движения.
При уровнях удобства движения А и Б расчет потерь времени целесообразно вести с использованием вероятностной модели движения потока автомобилей, разработанной автором и Л. Н. Сапегиным. Пусть поток, состоящий из быстрых и медленных автомобилей, поступающий с горизонтального участка дороги на подъем протяжением Ь, имеет следующие характеристики; д\; у\; дбб; "о;
1об (обозначения те же, что и в п. VIII.!). Как уже было найдено в п. VIII.!, вероятность того, что за медленно движущимся автомобилем перед подъемом уже имеется очередь из 1г быстрых автомобилей, составляет
![]()
где /г=0, 1; 2...
Обозначим через б/ продолжительность продвижения очереди автомобилей вдоль подъема на расстояние, равное динамическому габариту /а автомобиля:
м=г(")/1,(")
а / 1 ,
где ^м) — динамический габарит медленно движущегося автомобиля на подъеме;
^")—скорость медленно движущихся автомобилей на подъеме.
За время б< к очереди с вероятностью е =9бб(Vб~Vм) ъ( может пристроиться еще один быстро движущийся автомобиль, а с вероятностью р==1—в очередь останется прежней, т. е. конец очереди продвинется по подъему на величину 1^. В первом случае, когда к очереди подойдет еще один быстро движущийся автомобиль, конец очереди останется на месте. Вероятность прихода за
время Ы двух и более быстро движущихся автомобилей незначительна.
Обозначим через «м == Ь/1ц число медленно движущихся
автомобилей, которые могут разместиться на подъеме протяжением Ь.
Положение конца очереди будем изображать точкой на оси (рис. VIII.3), где 0 — нижняя точка подъема (начало подъема и конец вогнутой вертикальной кривой). Если в момент прохождения медленным автомобилем точки 0 за ним имеется очередь из Н быстрых автомобилей, то конец очереди находится в точке
—И. Требуется найти длину очереди в момент, когда конец очереди достигает высшей точки подъема.
Длина очереди быстро движущихся автомобилей на подъеме может быть получена следующим способом. Обозначим через М(—1г) среднюю длину очереди от точки —и до га. Тогда по формуле полного математического ожидания получаем:
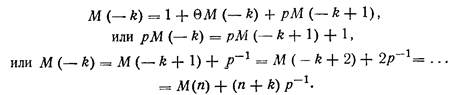
Учитывая, что М(п)=0, получим
![]()
Отсюда длина очереди в момент прохождения концом очереди точки п составит
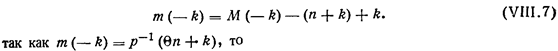
средняя длина очереди
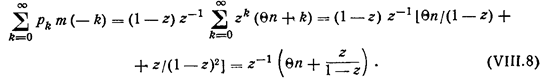
Потеря времени на подъеме одним быстро движущимся автомобилем
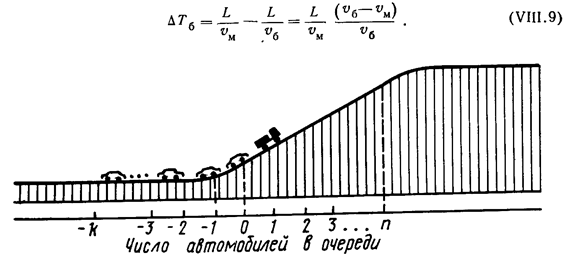
Рис. УШ.З. Схема перемещения очереди вдоль подъема
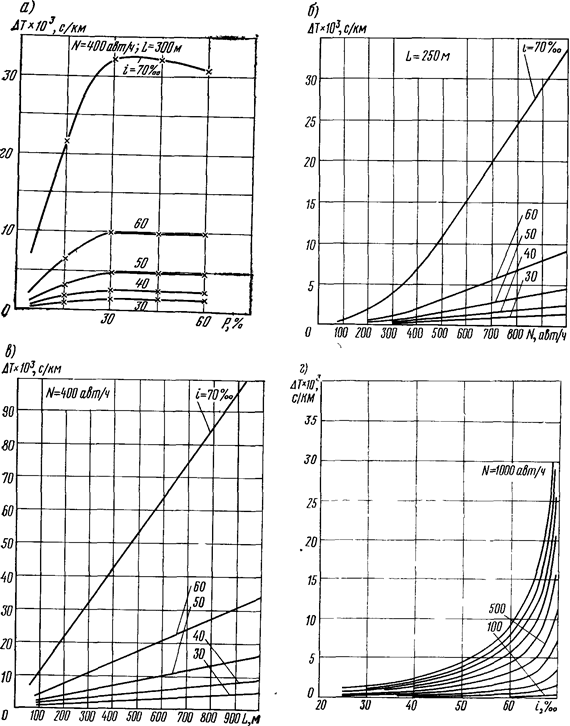
Рис. УП1.4. Потери времени на подъемах с различным уклоном-^Гпо^Т^^^ияУи^в^чи^-укТоТ^ интенсивности Д———ния, . - влияние дл„-
Потеря времени всеми быстро движущимися автомобилями, находящимися в очереди,
|
Продольный уши, %. 713 60 Я V 30 |
|
|
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.