На рис. МША показаны зависимости потери времени автомобилями для различных подъемов. Из этих графиков видно, что теоретические и фактические данные совпадают достаточно хорошо при интенсивностях до 500 авт/ч. На основе таких графиков была построена номограмма для определения потерь времени (рис.УП1.5).
|
|
Среднюю скорость движения быстро движущихся автомобилей на подъемах определяют по величине потери времени (УШЛО) из следующих соображений:
ДУ^з-^,, (уш.п)
где ДГ — потери времени быстро движущимися автомобилями, рассчитанные по уравнению (VIII.10); <з — время, затрачиваемое быстро движущимися автомобилями на преодоление подъема при наличии других автомобилей, зависит от интенсивности движения; (ев — время, затрачиваемое быстро движущимися автомобилями на преодоление подъема при отсутствии медленно движущихся автомобилей.
Из уравнения (VIII. 11) имеем ^з^св+А7'. (УШ.12)
Отсюда средняя скорость движения в зависимости от количества медленно движущихся автомобилей:
![]()
Влияние медленно движущихся автомобилей в уравнении (VIII. 13) учитывается через величину ДГ.
Из приведенных выше графиков видно, что наиболее благоприятные условия движения наблюдаются при уклонах менее 25%о и длине подъема менее 400 м.
VIII. 3. УСЛОВИЯ ПРИМЕНЕНИЯ ДОПОЛНИТЕЛЬНЫХ ПОЛОС НА ПОДЪЕМЕ И ИХ ПАРАМЕТРЫ
Устройство дополнительных полос на подъеме является наиболее эффективным мероприятием по увеличению пропускной способности этого участка. Вопрос об устройстве дополнительной полосы должен решаться на основе оптимального уровня удобства движения на дороге (см. п. VII.4).
Целесообразность устройства дополнительной полосы на подъеме можно определить по номограмме (рис. УШ.б). Так, например, для уклона 60°/оо, количества автомобилей, медленно движущихся 90 и быстро движущихся 165, при длине подъема 300 м (точка А на рис. VIII.6) и более необходимо устройство дополнительной полосы. Номограмма была получена на основе анализа потерь времени (см. п. УП1.2).
|
|
Можно выделить следующие основные параметры дополнительной полосы, которые требуют индивидуального подхода для их определения (рис. ¥111.7):
/I — зона перехода от двух к трем полосам;
/а — минимально-допустимая длина полосы перед подъемом при заданных интенсивности и составе движения;
!з— зона ограничения выхода с дополнительной полосы на скоростную полосу в пределах подъема;
|
|
4 — участок полосы за подъемом, требуемый для разгона медленно движущихся автомобилей и их встраивания в общий поток;
|
|
/5—зона перехода от трех к двум полосам.
На основе анализа натурных наблюдений и опытных проездов ходовой лаборатории были установлены протяженности элементов полосы /I, 1з, 1ь. Величины /а и /4 определялись с помощью методов теории массового обслуживания.
|
|
Для свободных условий движения можно принять
l1 ≈0,9v, (VIII.14)
где v — скорость движения перед подъемом, км/ч
Величина зоны перехода от трех к двум полосам определяется возможностью и удобством встраивания в основной поток движения.
Отмечено, что наилучшие условия встраивания обеспечиваются при угле а, равном 5°, т. е.
/5=B tq α, (VIII. 15)
где В — ширина дополнительной полосы, м.
Длина зоны огфаничения выезда с дополнительной полосы на полосу основного потока в пределах подъема в основном зависит от длины подъема Lп, наличия кривых в плане R на подъеме и расстояния видимости в сторону спуска. Наблюдениями установлено, что
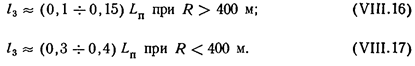
За подъемом эта зона продолжается на расстоянии 30—50 м.
Длины элементов 1ч и Ц зависят от интенсивности, состава и скорости движения.
Длину элемента 1ч при длине подъема до 500 м и интенсивности движения до 350 авт/ч следует принимать равной нулю. При значительных интенсивностях (более 400 авт/ч) величину 1ч можно назначать равной длине очереди, накапливаемой за медленно движущимся автомобилем во время его движения вдоль всего подъема (см. п. VIII.2).
При большом протяжении подъема (более 500 м) длина полосы /п в пределах подъема может быть определена из начального условия, что быстро движущийся автомобиль, следующий за медленно движущимся в среднем на расстоянии \|^б (^б — плотность потока быстрых автомобилей, авт/км), не успевает его догнать в пределах подъема.
Пусть быстро движущийся автомобиль имеет скорость ие на подходе и не теряет ее на подъеме. Медленно движущийся автомобиль теряет свою скорость им по следующему закону:
им (I) = им— аЛ.
Предположим, что быстро движущийся автомобиль догоняет медленно движущийся на расстоянии 5 от начала подъема. Тогда
время, в течение которого быстрый автомобиль догонял медленный, составит
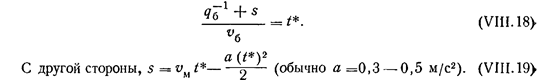
Подставляя выражение (VIII.18) в формулу (VIII.19), получаем
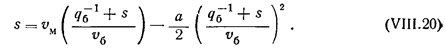
Решая полное квадратное уравнение (VIII.20), находим

Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.