Методические указания к лабораторным работампо курсу «Информационно-измерительные системы», страница 36

Рисунок 4.2 – Дифференциальные законы распределения случайных величин x₁ и x₂.

Для рассматриваемого случая когерентного приема двоичных сигналов с пассивной паузой с учетом (4.5) – (4.7) полная вероятность ошибки

.   (4.8)

После соответствующих преобразований [1] получим

,                                       (4.9)

где 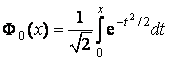 – функция нормированного и центрированного гауссовского распределения (функция Лапласа);  – отношение сигнал/шум в канале связи.

Графические зависимости (рис. 4.2) могут служить иллюстрацией изменения помехоустойчивости оптимального приемника в зависимости от выбранного порога k₀ и энергетического отношения сигнал/шум h ².

Так, при выборе  заштрихованная площадь, характеризующая полную вероятность ошибки, будет минимальной. При выборе другого порога (например, k₀^*) к заштрихованной области добавляется зачерченная область. Хотя при этом уменьшается вероятность пропуска, зато значительно увеличивается P_л.т.

Из (4.9) можно сделать вывод, что помехоустойчивость оптимального приемника зависит лишь от отношения энергии сигнала Q_c к спектральной плотности шума N₀ и не зависит от формы сигнала S(t).

Исследования показывают, что для сигналов с активной и пассивной паузами при когерентном приеме выражение для полной вероятности ошибки можно записать в универсальном виде

,                                           (4.10)

где g_с — постоянный коэффициент, значение которого зависит от способа модуляции сигналов.

Трудность осуществления описанной процедуры решения (4.4) состоит в том, что для ее реализации необходимо на приемной стороне создать колебания S(t), совпадающие с переданными колебаниями по амплитуде, частоте и длительности посылок (с точностью до фазы). Это сдерживает широкое применение когерентных методов приема.