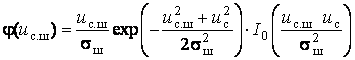Методические указания к лабораторным работампо курсу «Информационно-измерительные системы», страница 24

         ,                               (3.3)

где s_ш² — дисперсия шума; I₀ — функция Бесселя нулевого порядка от мнимого аргумента.

Распределение (3.3) также называют обобщенным распределением Релея. При отсутствии сигнала распределение (3.3) принимает вид

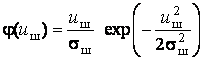         ,  так как  I₀ = 1.                      (3.4)

Полученная зависимость носит название «распределение Релея» и описывает плотность вероятностей огибающей нормального шума.

Введем обозначения: u_с.ш /s_ш = h;  u_с /s_ш = q;  u_ш /s_ш = z.

Тогда (3.3) и (3.4) примут вид

;                                   (3.5)

.                                             (3.6)

На рис. 3.2 приведены зависимости j(h) и j(z). При увеличении q кривая j(h) смещается вправо, приближаясь к нормальному закону распределения.

С учетом (3.1), (3.2) и (3.5), (3.6) выражение для вероятности ошибки при некогерентном приеме простых АМ-сигналов можно записать в виде

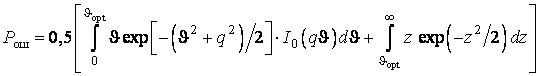.   (3.7)

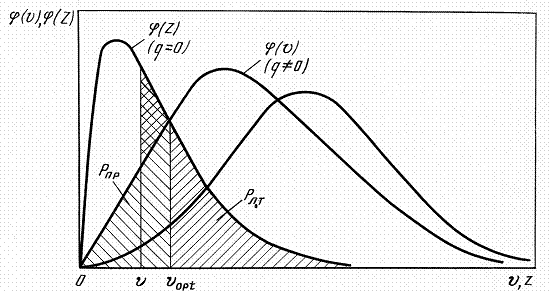
Рисунок 3.2 – Дифференциальные законы распределения
колебаний на выходе детектора огибающей

Выражение для оптимального порога можно получить, исследуя функцию (3.7) на минимум. Однако эту задачу можно решить проще. Как видно из рис. 3.2, минимальное значение вероятности ошибки обеспечивается при выборе порога на пересечении кривых j(z) и j(h). Любое изменение порога увеличивает полную вероятность ошибки на значение, соответствующее площади зачерченного криволинейного треугольника. Анализ различных способов модуляции при некогерентном приеме двоичных сигналов показывает, что для достаточно больших отношений сигнал/шум (h > 4) и оптимальном пороге вероятность ошибки будет определяться следующими выражениями: