Методические указания к лабораторным работампо курсу «Информационно-измерительные системы», страница 31

Обратное преобразование  будет

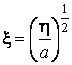.                                                      (3.19)

В случае если процесс  распределен нормально, с нулевым средним, т.е.

 ,                                 (3.20)

плотность  запишется как

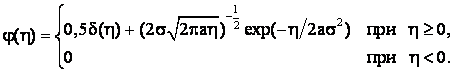     (3.21)

Графики нелинейных преобразований плотности распределения вероятностей приведены на pис. 3.7.

4.2 Подключить анализатор к выходу ограничителя 3. Полосу пропускания фильтра 2 сделать равной 10 кГц. Меняя типы нелинейности, снять по экрану осциллографа преобразованные законы распределения.

4.3 Включить квадратор 4. Подключив анализатор к выходу квадратора, снять по экрану полученный закон распределения.

4.4 Объяснить полученные результаты и сделать выводы.

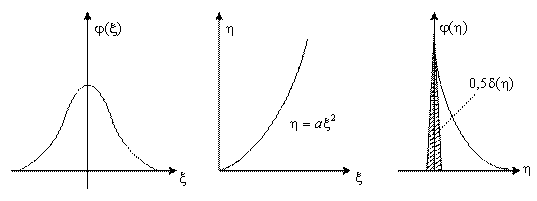
Рисунок 3.7 – построение закона распределения случайного процесса

на выходе квадрата

Опыт 5. Исследование закона распределения огибающей узкополосного процесса при различных отношениях сигнал/шум

5.1 Подключить анализатор к выходу приемника 8. Установив заданное соотношение мощности сигнала к мощности шума, снять законы распределения для случаев:

а) отсутствия сигнала передатчика 5 в канале связи 6 (плотность распределения Рэлея).

б) наличия сигнала передатчика в канале связи (плотность распределения Райса).

в) наличия сигнала передатчика в канале связи  (нормальный сигнал распределения).

5.2 Сделать выводы.

Содержание отчета

1. Функциональные схемы фотооптического анализатора (рис. 3.4) и макета (рис. 3.5).

2. Результаты опытов 2–5 с выводами.

3. Перечень оборудования, используемого в работе.

Список рекомендуемой литературы