Методические указания к лабораторным работампо курсу «Информационно-измерительные системы», страница 30

Переходя от приращений к дифференциалам, запишем

,                                                         (3.13)

откуда

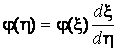.                                                        (3.14)

Рисунок 3.6 – Построение закона распределения случайного процесса

на выходе ограничителя

Если для функции  существует обратная функция , то выражение (3.14) перепишется как

.                                                  (3.15)

Рассмотрим теперь конкретные нелинейные преобразования случайного процесса.

А) Ограничение.

Пусть двухсторонний ограничитель имеет характеристику

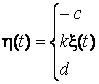
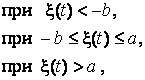                                 (16)

где a, b, c, d, k – постоянные числа.

На интервале (– c, d) преобразование  будет линейным (см. рис. 3.6). Поэтому внутри этого интервала

.                                                        (3.17)

В точках -c и d плотность  преобразуется в дельта-функции  и  амплитудами, пропорциональными отсекаемым площадям  и  соответственно.

Б) Возведение в квадрат.

Пусть односторонний квадратичный детектор имеет характеристику

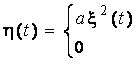
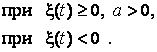                                (3.18)