Основы физики твердого тела: Учебное пособие (содержит конспект лекций и практическую часть), страница 7

При образовании кристалла происходит не только уменьшение высоты и ширины потенциального барьера, но и качественное изменение энергетических уровней электронов. Для выяснения этого воспользуемся соотношением неопределённостей Гейзенберга:

                       ,

где Dt – время нахождения электрона в энергетическом состоянии с энергией от E до E±DE, а величина DE определяет ширину энергетического уровня. В изолированном атоме электрон в основном  состоянии может находиться сколь угодно долго, и поэтому ширина энергетического уровня DE сколь угодно мала. В возбуждённом состоянии электрон находится в течение времени Dt = 10^-8 с и, следовательно, ширина возбуждённого энергетического уровня составляет для валентного электрона

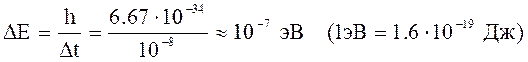
      U

                                                                                                                                                                                                                                                        r

                                 U₀

                                                  l

                                                 r=a

Рис. 2.2

Рассмотрим возможность оценки ширины DE разрешённых энергий валентного электрона в кристалле. Для простоты предположим, что потенциальный барьер, разделяющий атомы в кристалле, имеет прямоугольные стенки (рис. 2.3). Квантовая механика приводит к возможности прохождения частиц через потенциальный барьер, причём, прозрачность барьера D зависит от высоты  (U₀-E) и ширины ( l ) потенциального барьера, согласно формуле

                                                      (2.1)

В формуле (2.1) параметр D₀ по порядку величины равен единице. Для случая валентных электронов имеем:

масса электрона             m = 9.1×10^{-31 кг,}

полная энергия              E = 10 эВ,

ширина барьера             l = 10^-10 м,

высота барьера              U₀ – E = 10 эВ.    

Если принять, что скорость V электрона в потенциальной яме (атоме) равна 10⁵ м/с, то за одну секунду электрон n₀ = V/r раз ударится о барьер (правильнее здесь говорить о том, что электрон-волна будет отражаться от стенок барьера). Тогда частота просачивания электрона через потенциальный барьер определится как    ν = ν₀ D = VD/r. Отсюда время принадлежности валентного электрона конкретному атому равно         

.

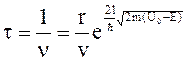Подстановка всех числовых значений в последнее выражение даёт величину для t = 10^-15 с. Применяя снова соотношение неопределённостей, для DE получим значение » 1эВ.

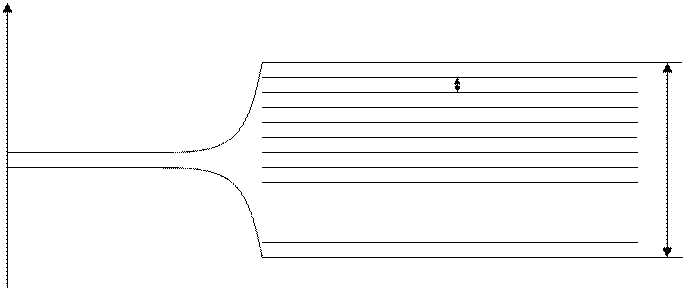
Таким образом, в кристалле возникает зона дозволенных значений энергии валентного электрона в 10⁷ раз шире, чем у этого же электрона в изолированном атоме (рис. 2.3). Говорят, что энергетический уровень электрона в изолированном атоме при образовании кристалла расщепляется в зону.

U

U₀

                                                                                       r                                 r

Рис.2.3

E                                                                                             10^-23 эВ

10^-7эВ                                                                                                               1эВ

    3s-уровень

                                                           3s-зона                  N-подуров.

Рис.2.4

Вследствие резкого уменьшения толщины и высоты потенциального барьера при сближении атомов свободу перемещения по кристаллу получают не только валентные электроны, но и электроны, расположенные на других энергетических уровнях атомов. Перемещение происходит путем  туннельного перехода их сквозь потенциальные барьеры, отделяющие соседние атомы. Чем тоньше и ниже эти потенциальные барьеры, тем полнее осуществляется обобществление электронов. Но чем меньше энергия электрона в атоме, тем больше он связан с ядром, тем больше для него размеры потенциальных барьеров. Так для электронов 1s-состояния время принадлежности конкретному атому составляет уже t ~ 10²⁰ лет, следовательно, они остаются в кристалле столь же жёстко локализованными на определённых узлах кристаллической решётки, как и в изолированном атоме.