Более того, если у идеального газа при Т = 0 энергия всех частиц обращается в нуль, то в металле в состоянии с нулевой энергией может быть не более 2-х электронов. Здесь действует неумолимый принцип Паули, и в результате все остальные электроны вынуждены занимать в зоне состояния с более высокими энергиями (рис. 3.3а). Но в высших состояниях кинетическая энергия весьма заметна и для большинства металлов лежит в пределах (3-7) эВ. Это соответствует скоростям порядка 106 м/с. Идеальный газ при столь высокой энергии частиц имел бы температуру 80000 К (Е = 3/2 kТ). Это явление известное под названием вырождение электронного газа было впервые открыто Э. Ферми. Основным признаком вырождения газа является независимость энергии его частиц от температуры (рис. 3.6). Электронный газ в металле будет вырожден до тех пор, пока любой из его электронов не сможет обмениваться энергией с кристаллической решеткой. Это станет возможным лишь тогда, когда энергия тепловых колебаний решетки kТ станет не меньше энергии Ферми, т.е.
.
Температура
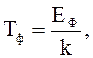
ниже которой газ находится
в вырожденном состоянии, носит название температуры вырождения или фермиевской
температуры. В табл. 1 приведены значения ТФ для ряда металлов. Так
как температура вырождения для любых металлов очень высока (
50000 К), то в обычных условиях электронный
газ в металлах является всегда вырожденным и описывается распределением
Ферми-Дирака.
С невырожденным электронным газом приходится иметь дело в собственных и слаболегированных полупроводниках, так как концентрация электронов в них значительно меньше, чем в металлах (в полупроводниках концентрация электронов колеблется от 1016 – 1019 до 1023 – 1024 м-3, а в металлах она составляет 1028 м-3). При таких концентрациях выполняется условие невырожденности и электронный газ оказывается невырожденным; при этом он подчиняется обычной статистике идеального газа – статистике Максвелла-Больцмана, которая описывается функцией распределения
.
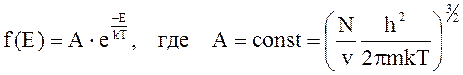3.7. Распределение Бозе – Эйнштейна
Функция распределения для бозонов имеет следующий вид:
.
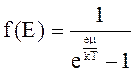(3.2)
Формула (3.2) носит название распределения Бозе – Эйнштейна. Бозоны не подчиняются принципу Паули. При Т = 0 все они стремятся занять уровень минимальной энергии. Бозоны «любят» накапливаться в одном состоянии, они являются «коллективистами». К бозонам относятся фотоны и фононы. Рассмотрим некоторые свойства бозонов на примере поведения фотонов.
1. Масса покоя фотонов равна нулю.
2.
Все фотоны движутся с одной и той
же скоростью, равной скорости света, но могут обладать различной энергией Е,
импульсом p; которые зависят от частоты 
:
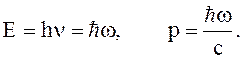
3. Фотоны не сталкиваются между собой. Равновесное распределение в фотонном газе может устанавливаться только в присутствии тела, способного излучать и поглощать фотоны. В процессе поглощения и последующего излучения фотоны одних частот превращаются в фотоны других частот.
4. Фотоны могут поглощаться и излучаться в любых количествах. Поэтому число фотонов в фотонном газе не является строго фиксированным и зависит от состояния газа. При заданных объеме и температуре в равновесном состоянии газ содержит такое число фотонов, которое обеспечивает минимум энергии в газе.
5. Химический потенциал равновесного фотонного газа равен нулю: 
.
4. МЕТАЛЛЫ
4.1. Теплоемкость электронного газа
Электронная теория металлов, развитая на основе квантовой механики, позволила правильно вычислить теплоемкость металлов. Исходя из классических представлений об электронном газе, его молярная теплоемкость должна быть равна
.
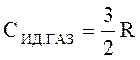Поскольку металл представляет собой совокупность решетки, в узлах которой находятся положительно заряженные атомные остатки, и электронного газа, то теплоемкость металлов, следовательно, должна быть равна:
.
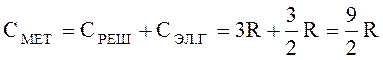Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.