Основы физики твердого тела: Учебное пособие (содержит конспект лекций и практическую часть), страница 15

Опыт показывает, что теплоемкость металлов, как и всех твердых тел, равна 3R. Отсюда следует, что теплоемкость электронного газа пренебрежимо мала по сравнению с решеточной, которая обусловлена переносом тепла фононами.

          Можно приближенно оценить величину электронной теплоемкости. При повышении температуры, как показано выше, увеличат свою энергию не все электроны, а только те, которые находятся в двойном энергетическом слое 2kT, расположенном около уровня Ферми (рис. 3.3б). Доля этих электронов от общего числа электронов проводимости составляет величину 2kT/E_Ф. Если бы все электроны проводимости вносили вклад в теплоемкость, то она была бы равна 3R/2 (для одновалентного металла). Принимая во внимание, что только часть электронов участвует в теплоемкости, запишем для электронной теплоемкости

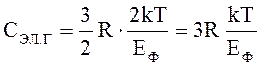                             (4.1)

Учитывая, что E_Ф = kT_Ф, перепишем выражение (4.1) в виде:

.                                         

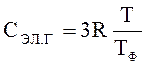Более точный квантовомеханический расчет дает для теплоемкости электронного газа формулу

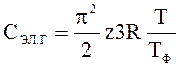                                                           ,                            (4.2)

где величина z определяет число валентных электронов, приходящихся на каждый атом металла.

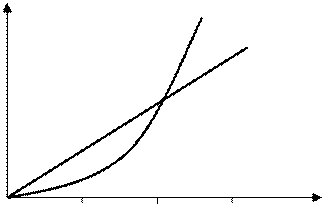
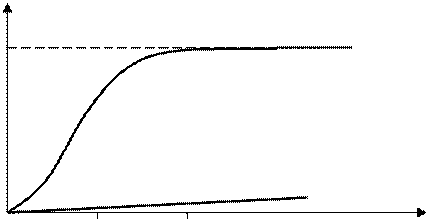
          Выражение (4.2) показывает, что величина теплоемкости электронного газа очень мала при любых температурах, так как Т << Т_Ф. Кроме того величина С_ЭЛ.Г  линейно возрастает с увеличением температуры. Качественное сравнение решеточной теплоемкости металлов с теплоемкостью электронного газа при больших и очень малых температурах  показано на рис. 4.1.

C                                                                                                             С_реш.~T³

3R                                                           C_ееш.        С                                     C_эл.г.~T

                                                         C_эл.г

                   150            300                                      T, K                 1           2                    3       T, K

Рис. 4.1

     Вклад электронов в теплоемкость металлов становится заметным только при очень низких температурах (Т < Q/50 ), где теплоемкость кристаллической решетки, пропорциональная Т³, становится даже меньше электронной теплоемкости, пропорциональной Т (Q- характеристическая температура Дебая).

4.2 Теплопроводность и электропроводность металлов

Опыт показывает, что теплопроводность металлов значительно больше теплопроводности диэлектриков.

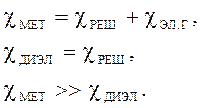
(- коэффициент теплопроводности). Это объясняется тем, что в металлах перенос тепла осуществляют свободные электроны, но нужно учесть, что в теплообмене участвуют не все электроны проводимости, а только их часть, как это указывалось выше.

          Как решеточную, так и электронную теплопроводность можно описать одинаковыми формулами:

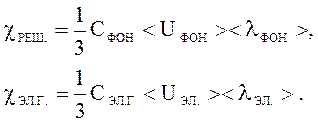
где С – молярная теплоемкость решетки и электронного газа соответственно, <U> - скорость фононов и электронов, <> - длина свободного пробега. Эти величины для кристаллов имеют такие значения, что

,

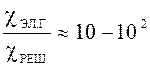т.е. электронная теплопроводность на 1 – 2 порядка больше решеточной.

          Электрическое сопротивление проводника в квантовой теории так же, как и в классической теории, объясняется взаимодействием электронов проводимости с кристаллической решеткой. В создании электрического тока участвуют все электроны проводимости. Вакантные состояния при действии внешнего электрического поля создаются сразу для всех электронов проводимости, так как каждый электрон, переходя в вакантное состояние, оставленное другим электроном, оставляет после себя такое же вакантное состояние, которое занимается третьим электроном и т.д.

4.3  Сверхпроводимость металлов