Строго говоря, в последнем выражении вместо массы m частицы стоит эффективная масса частицы m*. Введение эффективной массы частицы дает возможность учитывать сложный характер взаимодействия частицы с кристаллической решеткой при ее движении под действием внешнего электрического поля и при этом пользоваться привычными формулами. Эффективная масса частицы не определяет ни ее инертных, ни гравитационных свойств. Эффективная масса – это масса такой свободной частицы, которую она должна иметь для того, чтобы под действием внешней силы приобрести такое же ускорение, как и частица в кристалле под действием той же силы. Эффективная масса свободного электрона равна его действительной массе me*= me.
Наиболее характерной особенностью эффективной массы частицы в кристалле является то, что ее величина зависит от направления движения частицы и от ее состояния. Эффективную массу частицы можно экспериментально измерить.
3.5. Квантовая статистика электронов в металле (распределение Ферми-Дирака)
С точки зрения внутреннего строения металлы представляют собой решетку, в узлах которой расположены положительные атомные остатки и электронный газ, образованный из валентных электронов атомов. Концентрация свободных электронов имеет порядок 1022 – 1024 электронов в 1см3. Многие свойства металлов, в частности электрические, определяются состоянием свободных электронов. Поэтому основной задачей квантовой теории металлов является выяснение закономерностей в распределении свободных электронов по энергиям.
В основу квантовой статистики электронов в металле положены следующие основные принципы:
- все электроны одинаковы, т.е. не различимы;
- состояние электрона определяется набором четырех квантовых чисел,
- изменение состояния электрона определяется изменением хотя бы одного из квантовых чисел;
- электроны подчиняются принципу Паули: в системе не может одновременно более одного электрона в данном квантовом состоянии.
По классической электронной теории считается, что при Т = 0 в отсутствии внешних возбуждений энергия свободных электронов должна быть равна нулю, т.е. все электроны должны находиться в одном квантовом состоянии. Квантовая статистика отрицает возможность такого случая. Свободные электроны при указанных условиях находятся в различных квантовых состояниях и заполняют дискретные энергетические уровни разрешенной (валентной) зоны, начиная с самого нижнего до некоторого уровня. Этот последний уровень, занятый электронами, носит название уровня Ферми (рис. 3.3а). Энергия, соответствующая этому уровню, называется энергией Ферми. Таким образом, энергия Ферми – это максимальная энергия, которую может иметь электрон в металле при температуре абсолютного нуля.
Как уже говорилось, вероятность заполнения электронами энергетических уровней в условиях термодинамического равновесия электронов в системе определяет функция распределения f(E). Для случая вырожденного газа фермионов она впервые была получена итальянским физиком Э. Ферми и английским физиком Дираком и имеет следующий вид:
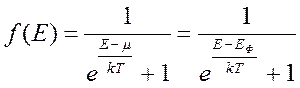. (3.1)
Формула
(3.1) определяет распределение Ферми-Дирака. Входящие в формулу
величины: k – постоянная Больцмана, Т – абсолютная температура, Е
– полная энергия электрона, m - химический потенциал.
Химический потенциал равен изменению энергии изолированной системы постоянного
объема при изменении в ней числа частиц на единицу: μ=dE/dN. В
случае вырожденного газа фермионов химический потенциал равен энергии Ферми ЕФ
.
Исследуем функцию (3.1). Если температура металла равна абсолютному нулю (Т = 0), то для значений полной энергии Е < ЕФ функция f(E) =1, а для значений Е > ЕФ функция f(E) =0 (рис. 3.4а). Это означает, что уровни, расположенные ниже уровня Ферми, обязательно заняты электронами (вероятность заполнения равна единице); уровни, расположенные выше уровня Ферми, свободны (вероятность заполнения равна нулю). Если температура металла отлична от нуля, то при
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.