Формула Дебая хорошо передаёт ход теплоёмкости с температурой лишь для тел с простыми кристаллическими решётками. У твёрдых тел со сложной структурой спектр колебаний чрезвычайно сложен.
1.6. Фононы
Подобно энергии электромагнитных волн, энергия тепловых волн также квантована. Квант энергии тепловых колебаний решётки называют фононом. Поле упругих волн, заполняющих кристалл, можно трактовать как газ, образованный квантами колебаний решётки – фононами. С этой точки зрения нагретый кристалл можно уподобить ящику, заполненному фононным газом. Фонон обладает энергией
![]()
и импульсом
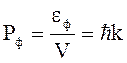 .
.
где k = 2p/l - волновое число, V – скорость фонона, равная скорости звука в твердом теле.
Фононы – квазичастицы. Квазичастицей называется частица, существующая только в веществе. Фононы – элементарные носители движения в системе частиц, входящих в кристаллическую решётку и связанных друг с другом силами взаимодействия. Распространяясь в кристалле, фононы рассеиваются при встрече друг с другом и с дефектами решётки. В случае теплового равновесия в кристалле одновременно может возбуждаться неограниченное число одинаковых фононов (принцип Паули на фононы не распространяется).
Дискретность дебаевских тепловых волн проявляется при температурах ниже характеристической температуры (Т < Q). При температуре абсолютного нуля особым состоянием движения является так называемое нулевое движение. особенность которого состоит в том, что оно не имеет дискретных характеристик, квазичастицы при этом как бы отсутствуют.
Свойства частиц и квазичастиц твёрдого тела и характер его нулевого движения определяют так называемый энергетический спектр твёрдого тела.
2. Зонная теория твёрдых тел
2.1. Модель свободных электронов
Для того, чтобы определить свойства кристалла, необходимо знать характер взаимодействия всех его частиц. Каждая частица входящая в 1 см3 кристалла, взаимодействует с 1023 – 1024 частиц, причём все они находятся в непрерывном и сложном движении.
Как известно, состояние любой квантовой частицы можно определить, решая соответствующее уравнение Шредингера. В случае взаимодействия всех составляющих кристалл частиц такая задача неразрешима. Она упрощается тем, что при описании ряда свойств кристалла, нужно знать только состояние его валентных электронов. Таким образом, многоэлектронная задача сводится, благодаря упрощениям, к одноэлектронной задаче о движении одного электрона в так называемом самосогласованном поле кристалла.
Упрощения сводятся к следующим положениям:
1. Поскольку скорость ядер много меньше скорости электронов, то движение ядер не учитывается, а рассматривается только движение электронов в поле неподвижных ядер.
2. Медленное движение ядер можно рассматривать в усреднённом поле, создаваемом средним пространственным распределением заряда электронов.
3. Взаимодействие одного электрона с остальными электронами рассматривается как взаимодействие этого электрона с самосогласованным полем, образованным усредненным пространственным распределением заряда электронов. В результате этих упрощений уравнение Шредингера разрешимо. Решение его даёт значения энергии электрона в кристалле. Заполнение электронами энергетических уровней происходит в соответствии с принципом Паули.
Модель свободных электронов, разработанная Друде и Лоренцем, явилась первой удачной попыткой объяснения электрических и магнитных свойств твёрдых тел (в первую очередь, металлов), но она оказалась бессильной при рассмотрении свойств твёрдых тел, зависящих от их внутренней структуры. Эта модель не давала ответа на такой вопрос, почему одни твёрдые тела являются проводниками, другие – изоляторами. Дальнейшим этапом в развитии электронной теории явилась зонная теория твёрдых тел, развитая Зоммерфельдом и другими учеными.
2.2. Расщепление энергетических уровней
изолированного атома в зоны при образовании кристалла
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.