N(E)dE = f(E)×g(E)×dE.
Функцию f(E) называют просто функцией распределения. Она выражает вероятность заполнения частицами данных состояний (или среднее число частиц, находящихся в данном состоянии). Таким образом, задача об отыскании полной функции распределения частиц по состояниям сводится к отысканию функций g(E) и f(E).
3.3. Понятие о фазовом пространстве
Представим себе классическую частицу. Её состояние можно определить заданием трёх координат (x, y, z) и трёх составляющих импульса (Px, Py, Pz). Состояние такой частицы в шестимерном пространстве с координатами x, y, z, Px, Py, Pz будет определяться точкой (x, y, z, Px, Py, Pz). Такое пространство называется фазовым, а определяющие состояние частицы точки называют фазовыми точками. Величина
DГ = DГy × DГp = dx dy dz dpx dpy dpz
называется элементом объема фазового пространства. Здесь DГy = dx dy dz представляет собой элемент объёма пространства координат, а DГp = dpx dpy dpz – элемент объёма пространства импульсов.
Для классических частиц удобно пользоваться не шестимерным фазовым пространством, а трёхмерным пространством импульсов, так как в этом случае DГy равно просто объёму V, в котором движутся частицы: DГy = V.
Для квантовых частиц дело обстоит иначе. Наличие у микрочастиц волновых свойств исключает, согласно принципу неопределённостей, возможность различать два состояния (x, y, z, Px, Py, Pz) и (x+dx, y+dy, z+dz, Px+ dPx, Py+ dPy, Pz+d Pz), если произведение dx dy dz dpx dpy dpz окажется < h3. Так как это произведение выражает элемент объема фазового пространства, то отсюда следует, что различным элементам объема шестимерного фазового пространства будут отвечать различные квантовые состояния микрочастицы лишь в том случае, если размер этих элементов объема не меньше h3. Поэтому в квантовой статистике за элементарную ячейку шестимерного фазового пространства принимается объем, равный
DГ = DГV DГP = h3.
Для классических частиц элемент трехмерного пространства импульсов равен
DГP = h3/V.
Процесс деления фазового пространства на ячейки конечной величины (h3 или h3/V) называют квантованием фазового пространства.
3.4 Плотность состояний
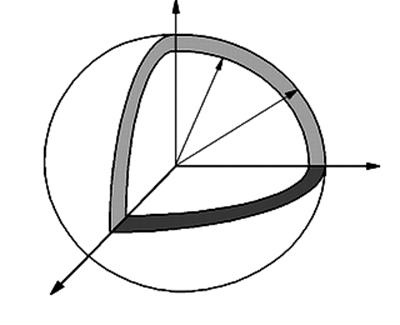
Подсчитаем число состояний, которым обладает микрочастица в интервале энергий от Е до Е+dЕ. Для этого проведем в пространстве импульсов две сферы радиусами р и р+dр. (рис. 3.1). Между этими сферами находится шаровой слой, имеющий объем, равный 4pp2 dp. Число элементарных фазовых ячеек в этом слое
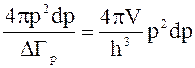 .
.
Так как каждой ячейке отвечает одно состояние микрочастицы, то число состояний, приходящееся на интервал dp, заключенный между р и р+dр, равно
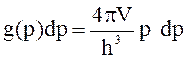 .
.
Для
невзаимодействующих частиц полная энергия 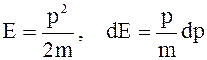 . Отсюда
. Отсюда
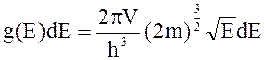 .
.
Плотностью состояния g(E) называется число состояний микрочастицы, приходящееся на единичный интервал энергий
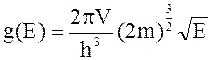 .
.
Из
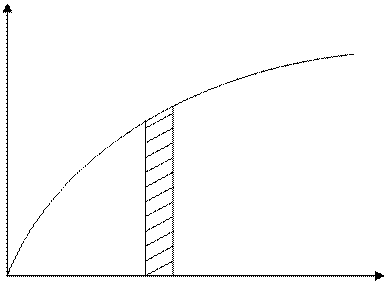
последнего выражения видно, что с ростом Е плотность состояний увеличивается
пропорционально ![]() (рис. 3.2).
(рис. 3.2).
 Pz
Pz
![]() g(E)
g(E)
![]() E P
E P
p+dP
![]() Py
Py
Px dE E
Рис. 3.1
Рис. 3.2
В случае электронов каждой фазовой ячейке отвечает два состояния, отличающиеся друг от друга направлением спина, поэтому для электронов плотность состояний следует удвоить
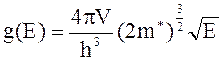 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.