Основы физики твердого тела: Учебное пособие (содержит конспект лекций и практическую часть), страница 20

           s = s_n + s_p = q×n(<U_n> +<U_p>) .                               (5.2)

q - заряд электрона, n – концентрация свободных электронов, равная в чистом полупроводнике концентрации свободных дырок; <U_n> и <U_p> - соответственно средние подвижности электронов и дырок. Подвижностью называется скорость носителей тока при напряжённости внешнего поля, равной 1 В/м.

Свободные носители заряда – электроны в зоне проводимости и дырки в валентной зоне - получили название собственных носителей тока, а обусловленная ими проводимость - собственной проводимости полупроводника.

Согласно (5.1) концентрация электронов и дырок в чистом полупроводнике нарастает согласно экспоненциальному закону

n = A exp (-DE /2kT),                                                   (5.3)

где А – некоторая постоянная величина, слабо зависящая от температуры при небольших Т. Подставляя (5.3) в (5.2), получим для проводимости полупроводника соотношение:

    s = s₀ exp (-DE /2kT),                                             (5.4)

в котором величина s₀ является постоянной, не зависящей от температуры. Таким образом, для собственных полупроводников наблюдается характерная температурная зависимость: их проводимость растёт с ростом температуры по экспоненциальному закону (напомним, что у металлов она уменьшается). Типичные температурные зависимости удельной электропроводности и сопротивления чистого полупроводника  показаны на рис. 5.1 и 5.2.

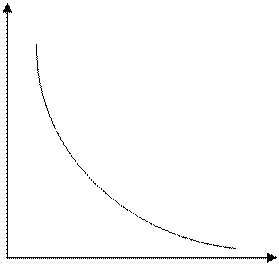
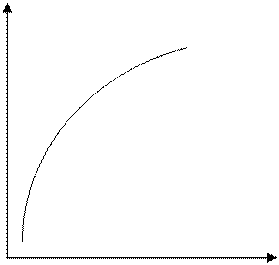   σ                    R

                                                    T                                                             T

                          Рис. 5.1                                                 Рис. 5.2

Зависимости s (Т) и  R (Т ) удобно представить в полулогарифмическом масштабе. Логарифмируя выражение (5.4), получим соотношение

                                               ln s = ln s₀ -DE /2kT.

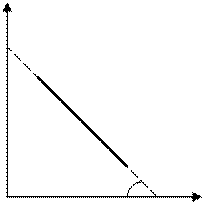
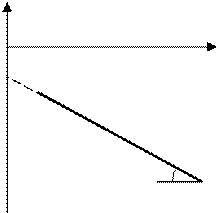
Если по оси абсцисс отложить 1/Т, а по оси ординат lns (или ln(1/R)), то получатся линейная зависимости (рис. 5.3).

        lnσ                    ln

        lnσ₀                                                           ln1/T

                                                                                                              a

                                a

                                                 1/T

Рис. 5.3

По тангенсу угла наклона этой прямой к оси абсцисс можно определить величину ширины запрещённой зоны, используя формулу

                        DЕ = 2kT tg a.                              

При достаточно высокой температуре собственная проводимость наблюдается во всех без исключения полупроводниках. Однако в полупроводниках, содержащих примесь, электропроводность слагается из собственной проводимости и примесной, причём собственная проводимость при этом много меньше примесной проводимости.

5.2. Примесная проводимость полупроводников

Примесная проводимость возникает в том случае, когда некоторые атомы исходного полупроводника заменить в узлах кристаллической решётки атомами примеси, валентность которой отличается от валентности основных атомов на единицу.

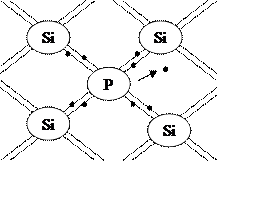
Электронная проводимость (полупроводники n – типа). Рассмотрим случай, когда атомы чистого полупроводника частично заменяются атомами примеси, валентность которой на единицу больше, чем валентность выбранного полупроводника. Например, атомы кремния (он четырёхвалентный) заменяются 5-валентными атомами фосфора. Для образования ковалентных связей с соседними атомами кремния атому фосфора достаточно четырёх электронов. Следовательно, пятый валентный электрон примеси оказывается как бы лишним и легко отщепляется от атома фосфора за счёт энергии теплового движения, образуя свободный странствующий электрон (рис. 5.4).

                                                                   E       зона проводимости

                                                                донорные уровни

                                                   валентная зона

           Рис. 5.4