Основы физики твердого тела: Учебное пособие (содержит конспект лекций и практическую часть), страница 4

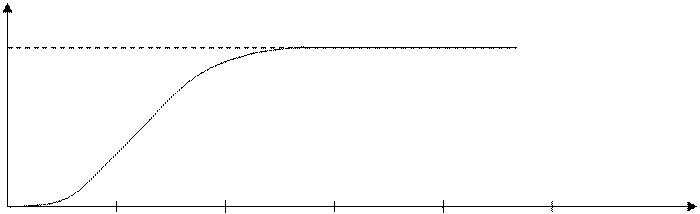
Действительно, в прошлом столетии французские физики Дюлонг и Пти (1819 г.) опытным путём установили, что теплоёмкость всех твёрдых тел не зависит от температуры и примерно равна 25 Дж/(моль×К). Это утверждение носит название закона Дюлонга и Пти. Дальнейшие исследования показали, что теплоёмкость твёрдых тел не зависит от температуры только в области высоких температур (Т ³ 300 К) и уменьшается с понижением температуры Т (рис. 1.4). С позиции классической теории нельзя объяснить зависимость теплоёмкости от температуры.

    С

    3R

                         100             200           300            400             500                               T, К

Рис. 1.4

Теория теплоёмкости кристаллических тел была создана А. Эйнштейном в 1907 году. Основные положения теории базировались  на модели твёрдого тела, по которой решётка из N атомов отождествлялась с системой N гармонических квантовых осцилляторов, колеблющихся с одинаковой частотой w. Тепловое колебание, как и всякое гармоническое колебание, можно разложить на  два поперечных и одно продольное. При определённой температуре в кристалле устанавливается система 3N колебаний. Эти колебания, достигнув поверхности кристалла, отражаются от неё и образуют стоячие волны, связанные с размером кристалла и его упругими свойствами. Число независимых стоячих волн в твёрдом теле равно 3N. Далее Эйнштейн полагал, что энергия колебательного движения осцилляторов, согласно гипотезе Планка, квантуется (e = n ħw). Для теплоёмкости Эйнштейн получил формулу.

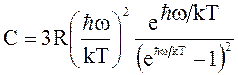,                          (1.1)                    

которая описывала экспериментальный график С(Т) вплоть до самых низких температур. В области абсолютного нуля формула (1.1) имела расхождение с экспериментом.

Рассмотрим два предельных случая формулы (1.1).

1).  kT >> ħw   (высокие температуры). В этом случае можно экспоненту разложить в ряд 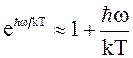 в знаменателе, а в числителе . В результате получается значение  С = 3R, что соответствует закону Дюлонга и Пти.

2). kT << ħw   (низкие температуры). В этом случае можно пренебречь единицей в знаменателе, и формула для теплоёмкости принимает следующий вид:

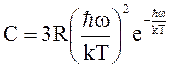
Множитель exp(-ħw/kT) изменяется намного быстрее, чем Т². Поэтому при приближении к абсолютному нулю теплоёмкость будет уменьшаться по экспоненциальному закону. Опыт же показывает, что вблизи абсолютного нуля теплоёмкость убывает по закону Т³. Следовательно, теория Эйнштейна не давала правильного хода теплоёмкости при самых низких температурах.   Количественного согласия с опытом удалось достигнуть Дебаю, который продолжил теорию Эйнштейна о представлении теплового движения атомов в виде 3N стоячих волн, но учёл, что колебания атомов не являются независимыми, поэтому осцилляторы колеблются с разными частотами. Диапазон частот этих волн широкий: w = (10² – 10¹³) Гц. Скорость распространения тепловых волн равна скорости звука. Энергия распределяется между всеми волнами, но большая часть энергии приходится на короткие волны. При низких температурах основной вклад в теплоёмкость по теории Дебая вносят колебания с низкой частотой. Формула Дебая для теплоёмкости твёрдых тел имеет вид:

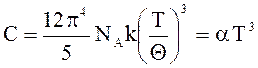                                                     (1.2)

При очень низких температурах теплоёмкость твёрдого тела пропорциональна Т³.  Зависимость (1.2) известна как “закон кубов Дебая”.

Важнейшую роль в теории Дебая играет понятие характеристической температуры (или температуры Дебая), которую можно определить как

            ,                                               

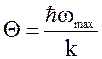где w_max – частота наиболее быстрых из 3N колебаний. Например,  для алмаза Q = 1860 К, для свинца Q = 90 К, для алюминия Q = 418 K. Характеристическая температура – важный параметр твёрдого тела. При температуре Дебая в твёрдом теле возбуждается весь спектр колебаний, включая колебания с максимальной частотой. Поэтому дальнейшее повышение температуры (Т > Q) не может уже вызвать колебаний с новыми частотами.