Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов

3. Основы теории графов

Теория графов находит самое широкое применение в моделировании информационных процессов, в программировании и в решении экономических задач. Она позволяет просто описывать сложные явления и дает им графическую интерпретацию. ”Картинка”  графа позволяет быстро понять проблему и на интуитивном уровне разработать рациональный алгоритм решения.

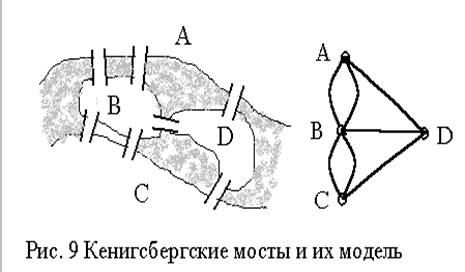          Первая работа по теории графов была опубликована математиком Л. Эйлером в 1736г. в Трудах Академии наук Санкт-Петербурга в виде задачи о Кенигсбергских мостах (см. рис. 9). Суть задачи сводилась к следующему: мог ли житель Кенигсберга, выйдя из дома, находящегося на части суши A, B, С или D, пройти по семи мостам через реку Прегель в точности по одному разу и вернуться домой? Ответ на этот вопрос был отрицательным.

          Для пояснения задачи представлена модель (см. рис. 9), где каждый участок суши замещен точкой на плоскости, а мосты – линиями,связывающими участки суши.

3.1. Граф и его характеристики

Итак, совокупность объектов произвольной природы и отношений между каждой парой этих объектов может быть изображена на плоскости в виде множества точек, являющихся образом множества объектов, и множества отрезков линий, соединяющих пары точек, что является образом множества отношений. Такой образ объектов и отношений принято называть графом. Множество точек, являющихся образом множества объектов, называют вершинами графа, а множество отрезков линий, являющихся образом множества отношений, - рёбрами или дугами графа.

Вершинами графа могут быть операторы программы или команды операционной системы, контактные площадки на плате компьютера, узлы транспортной или электрической сети, события в любой сфере человеческой деятельности, а рёбрами или дугами – связи операторов программы, команд операционной системы, контактных площадок на плате компьютера, узлов в транспортной или в электрической сети или причинно-следственные связи событий в любой сфере человеческой деятельности.

Граф может быть задан в двух формах:

а) G=<X, r>,

   где r={(x_i, x_j)| x_i, x_jÎX}Í(XÄX)  или

б) G=<X; h>,

   где h={{x_j}_Xi| x_i, x_j ÎX}Í(XÄX).

Первая форма применяется в тех случаях, когда необходимо отмечать дополнительные характеристики об отрезках линий, соединяющих вершины графа: протяжённость, загрузка, пропускная способность и т.п. Вторая форма применяется в тех случаях, когда необходимо отмечать характеристики о вершинах графа: время исполнения команды или оператора, надёжность контактной площадки или загруженность узла транспортной или электрической сети.

Граф G=<X; r> называют неориентированным, если (x_i, x_j)=(x_j, x_i).

Отрезок линии (x_i; x_j), соединяющий две вершины, называют ребром.

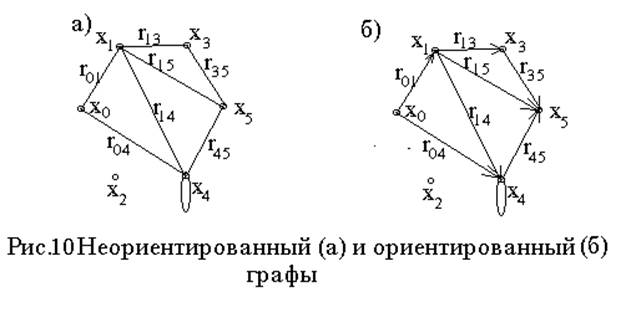
Граф G=<X; r> называют ориентированным, если (x_i, x_j)¹(x_j, x_i), а направленный отрезок линии (x_i; x_j), соединяющий две вершины,  называют дугой.   На рис. 10 приведены неориентированный и ориентированный графы.

Любая программа или алгоритм вычислительного процесса, электронная схема или последовательность операций производственного процесса могут быть представлены ориентированным графом, а любая схема транспортной или электрической сети - неориентированным.

Для определения отношения принадлежности вершин графа ребру или дуге и, наоборот, рёбер или дуг - вершине вводится понятие “инциденция”, т.е. вершина x_i  инцидентна ребру или дуге (x_i, x_j), если она является концевой вершиной данного отрезка линии, а ребро или дуга (x_i, x_j) инцидентна вершине x_i , если отрезок линии ограничен концевой вершиной x_i .

Число вершин, инцидентных ребру или дуге, всегда равно 2, т.к. они являются концевыми вершинами отрезка линии, а число рёбер или дуг, инцидентных вершине x_i, может быть произвольным. Это число называют степенью или валентностью вершины x_i и обозначают d_i=S_j(x_i, x_j). Число дуг, исходящих из вершины x_i, называют полустепенью вершины графа и обозначают d_i⁺=S_j(x_i, x_j)⁺. Вершину x_i, инцидентную исходящей дуге (x_i, x_j)⁺,  называют истоком( символ ”⁺” cвидетельствует о направлении дуги от вершины x_i). Число дуг, заходящих в вершину x_i, также называют полустепенью вершины графа и обозначают d_i^-=S_j(x_i, x_j)^-. Вершину x_i, инцидентную заходящей дуге (x_j, x_i)^-  , называют стоком ( символ ”^-” cвидетельствует о направлении дуги к вершине x_i).

Две вершины графа называются смежными, если они различны и между ними существует ребро или дуга. Вершина x_i, несмежная ни с одной вершиной графа, называется изолированной. На рис. 10 изолированной является вершина x₂ .

Два ребра также называются смежными, если они различны и имеют общую вершину.

Последовательность смежных рёбер или дуг, соединяющих вершины x_i и x_j , называют маршрутом и обозначают m_ij=((x_i, x_k);…. . . (x_l, x_j)). Например, для неориентированного графа, приведенного на рис. 10, между вершинами x₀ и x₅ существует шесть маршрутов, т.е. m₀₅={(r₀₄, r₄₅); (r₀₁, r₁₄, r₄₅); (r₀₁, r_1,5); (r₀₄, r₄₁, r₁₅); (r₀₄, r₄₁, r₁₃, r₃₅); (r₀₁, r₁₃, r₃₅)}.