Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 3

 Граф G’=<X’; r’> называют частичным для графа G=<X; r>, если он порождён подмножеством рёбер или дуг исходного графа G, т.е. r’Í r, вместе с инцидентными им вершинами, т.е. X’ÍX. Например, для графа (см. рис. 10а) подмножество рёбер r’={r₀₁, r₀₄, r₁₅, r₄₅} вместе с инцидентными им вершинами X’={x₀, x₁, x₄, x₅} формирует частичный  граф G’=<X’; r’> (см. рис. 15а)..

Граф G’=<X; r’> называют суграфом для графа G=<X; r>, если он порождён подмножеством рёбер и ли дуг графа G, т.е. r’Í r, и всеми вершинами графа G, т.е. X’ÍX. Например, для графа (см. рис. 10а) подмножество рёбер r’={r₀₁, r_04, r_15, r₄₅} вместе со всеми вершинами графа G формирует суграф G’=<X; r’> (см. рис. 15b). 

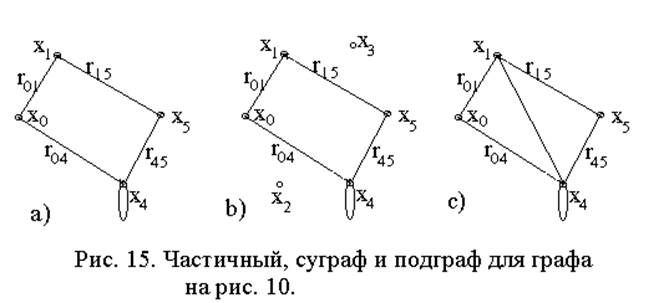Граф G’=<X’; r’> называют подграфом графа G=<X; r>, если он порождён подмножеством вершин исходного графа, т.е. X’ÍX, совместно с инцидентными им рёбрами или дугами. Например, для графа (см. рис. 10а) задание подмножества вершин X¢={x₀, x₁, x₄, x₅} вместе с инцидентными им ребрами формирует подграф G’=<X’; r’> (см. рис. 15с).

Суграф  G’=<X’; r’> связанного графа  G=<X; r>, формируемый без циклов, петель и кратных рёбер, называют остовом графа G=<X; r>.

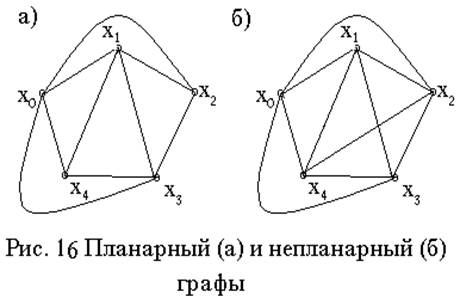Граф называют планарным, если он может быть изображён на плоскости так, что рёбра или дуги графа не пересекаются. Плоские графы используют при проектировании сетей телекоммуникации, особенно при проектировании печатных плат и т.п.

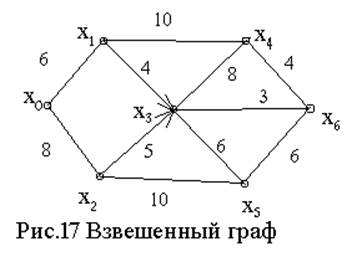Граф G=<X;r> называют взвешенным, если его рёбра или вершины имеют дополнительные характеристики: время исполнения команды операционной системы или оператора программы, вероятность наступления события или надёжность эксплуатации узла и т.п. определяют вес вершины графа, а протяжённость линий транспортных или электрических сетей, их пропускная способность по какому-либо параметру определяют вес ребра или дуги.

rij	(xi, xj)		xi	hxi={xj}	Граф может быть задан списочными или матричными структурами. При задании списком используют обе модели графа: G=<X; r> и G=<X; h>.
r01	(x0, x1)		x0	x1, x4
r04	(x0, x4)		x1	x3, x4, x5
r13	(x1,x3)		x2	-
r14	(x1, x4)		x3	x5
r15	(x1, x5)		x4	x5
r35	(x3, x5)		x5	-
r44	(x4, x4)
r45	(x4, x5)

Списки отношений удобны для хранения информации о весе ребра и поиска инцидентных вершин,а списки отображений - о весе вершины и поиска смежных вершин.

Матрица инциденции. Поскольку инциденция есть отношение принадлежности элемента одного множества X другому множеству r, то матрица инциденции ||q_i;j|| должна быть прямоугольной, число строк которой равно мощности множества отношений |r|=m, а число столбцов - мощности множества вершин графа |X|=n. Элементы матрицы инциденции неориентированного графа определяются по формуле:                    1, если (x_i, x_j) инцидентно x_j,

h_ij =

0, в противном случае.

Cледует отметить, что в каждой строке матрицы количество единиц равно двум, а в каждом столбце равно степени вершины - d_i (см. табл. а) для графа на рис. 10).