Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 23

pi	0	1	2	3	4	5	6	7	8
i	0	1	2	3	4	5	6	7	k
t0(i)	0	0	0	5	0	0	0	4	0

Алгоритм расчета резерва времени на работу.

шаг 1: принять р=0 и выделить любую дугу (i,j);

шаг 2: определить резерв времени для работы (i,j) по формуле:

t_i,j^0.=(t_n(j)- t_p(i)-t_j,i);

шаг 3: если р=m, где m-число дуг, то конец, иначе р=(р+1), выделить новую дугу (i,j) и перейти к шагу 2 алгоритма.

Результаты расчетов приведены в таблице.

pi	(i,j)	ti,j0	pi	(i,j)	ti,j0
1	(0,1)	0	7	(3,5)	5
2	(0,2)	6	8	(4,6)	2
3	(1,2)	0	9	(4,7)	4
4	(1,3)	5	10	(5,6)	0
5	(1,5)	8	11	(5,k)	3
6	(2,4)	0	12	(6,k)	0
			13	(7,k)	4

Произведенный анализ показывает, что

1) события 1, 2, 4, 5, 6, за которыми при исполнении проекта нужно следить с особым вниманием, имеют резерв времени равный нулю;

2) работы (0;1); (1;2); (2;4); (5;6); (6;k), которые лимитируют продолжительность исполнения всего проекта, имеют полный резерв времени равный нулю;

3) работы (0;2); (1;5); (4;6); (5;k) имеют резерв времени больше нуля, что позволяет уменьшить затраты трудовых, финансовых или материальных ресурсов и продлить исполнение этих работ, но не более указанных резервов.

Вопросы и задачи

rk	r1	r2	r3	r4	r5	r6	r7
(xi;xj)	(x1;x2)	(x1;x3)	(x2;x5)	(x3;x4)	(x2;x4)	(x4;x6)	(x5;x6)

3.  1 Граф задан списком отношений:

а) нарисуйте граф;

b) укажите разрез для X¢={x₁;x₂;x₄} и X\X¢={x₃;x₅;x₆};

c) нарисуйте частичный граф на рёбрах {r₂;r₄;r₆};

d)  нарисуйте суграф на рёбрах {r₁;r₃;r₅;r₇};

e)  нарисуйте подграф на вершинах x₂,x₄,x₅,x₆;

f)  составьте матрицу инциденции и матрицу смежности.

3. 2 Граф задан списком отображений :

xi	x	x	x	x	x	x	x	x	x
hXi	x2	x1 , x4	x4	x2,x3,x5,x6	x4 , x7	x4	x5,x8,x9	x7	x7

          а) нарисуйте граф;

b) укажите маршрут и переход из вершины  x₃ в вершину x₆;

c)  укажите разрез для X¢={x₁;x₂;x₄} и X\X¢={x₃;x₅;x₆};

d)  cоставьте матрицу инциденции и матрицу смежности.

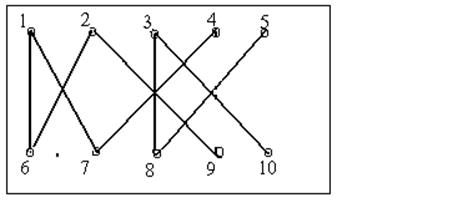
3. 3 Найти число компонент связности для графа

          3.4 Найти объединение и пересечение двух графов

r11	r21	r22	r23	r24	r25	r26
(xi;xj)	(x1;x2)	(x1;x5)	(x1;x4)	(x2;x3)	(x2;x4)	(x2;x5)

а) граф G₁=<X; r₁>

ri	r11	r12	r13	r14	r15	r16
(xi;xj)	(x1;x3)	(x2;x4)	(x2;x5)	(x3;x4)	(x3;x5)	(x4;x5)

б) граф G₂=<X; r₂>

]

         3.5  Найти цикломатические и хроматические числа, числа внутренней и внешней устойчивости для графов. Изоморфны ли графы?

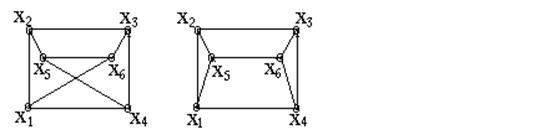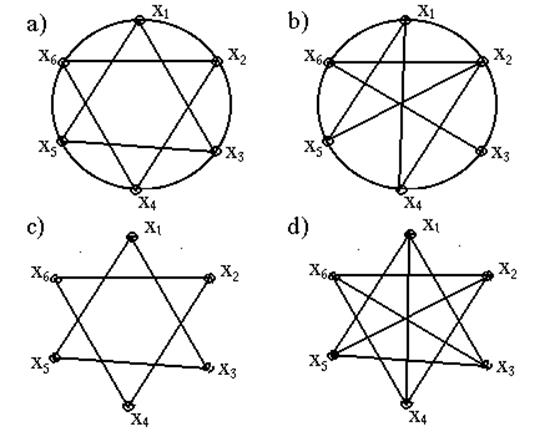
3.6 Для четырех графов найти: дополнение, числовые характеристики, объединение графов a и d, пересечение графов b и d, композицию графов c и d.

3. 8 По основным алгоритмам выполнить индивидуальные задания (см. Приложениям 1-5).