Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 18

По матрицам ||l⁷|| и ||n_i,j ⁷|| можно найти длину кратчайшего перехода между любой парой вершин исходного графа. Например, между вершинами х₀ и х₇ длина кратчайшего пути равна 18, а переход n₀₇=(х₀;х₃;х₂;х₄;х₇), между вершинами х₁ и х₆ длина кратчайшего пути равна 8, а переход n₁₆=(х₁;х₂;х₆) и т.д.

При решении практических задач возникает необходимость поиска нескольких путей, частично - упорядоченных по возрастанию относительно кратчайшего. Такие задачи возникают при временной загруженности канала на определенном участке или неисправности узла. Для решения подобных задач разработаны обобщенные алгоритмы Флойда.

3.4.4 Поиск максимального потока и его распределения в сети

При обмене информацией между абонентами вычислительной сети, при параллельных вычислениях на многомашинном комплексе, когда решение задачи распределено между несколькими процессорами, при использовании в вычислительной сети общей памяти, когда каждый процессор получает доступ к общим модулям на ограниченный отрезок времени, возникает задача передачи максимального объема информации в заданный отрезок времени. При работе транспортной системы, когда осуществляется обмен транспортными единицами между узлами сети возникает задача передачи максимального числа транспортных единиц в заданный отрезок времени. При передаче энергии в электрических сетях, жидкости в трубопроводных системах возникает задача распределения и передачи максимального объема энергии или вещества в заданный отрезок времени.

Объем информации, энергии или вещества, передаваемый от узла x_i к узлу x_j, называют потоком и обозначают j_ij.

Граф, являющийся образом транспортной системы, называют сетью. Особенностью сети является отсутствие петель и кратных дуг, ориентация всех отрезков линий, т.е. наличие дуг в графе, наличие вершины-истока и вершины-стока в сети.

Наибольший поток, который может пропустить дуга (x_i, x_j), называют пропускной способностью дуги и обозначают с_ij.

Очевидно, что 0£j_ij£ с_ij.

В вершине-истоке х₀ величина потока есть сумма потоков по всем дугам, исходящим из вершины х₀, т.е. j=å_ij_0i⁺.

В вершине-стоке х_k величина потока есть сумма потоков по всем дугам, заходящим в вершину х_k, т.е. j=å_ij_ik^-.

Для любой промежуточной вершины х_i сумма исходящих потоков равна сумме заходящих потоков, т.е. å_jj_ij⁺=å_kj_ik^-.

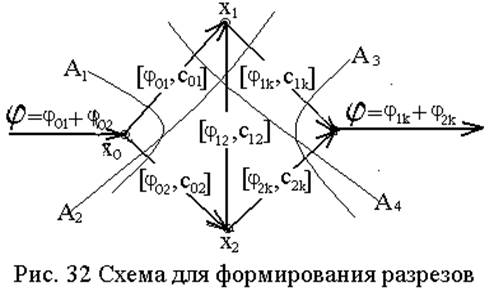
На рис. 32 показана условная сеть, содержащая вершину-исток х₀, вершину-сток х_k и две промежуточные вершины х_i и х_j. На каждой дуге в круглых скобках приведены обозначения потока и пропускной способности соответствующей дуги. При этом поток, подводимый к сети равен j=(j_0i+j_0j), поток отводимый от сети равен  j=(j_ik+j_jk), поток из вершины х_i в вершину х_j равен j_ij. Для вершины х_i  имеем  j_0i=(j_ij+j_ik), для вершину х_j -  j_jk=(j_0j+j_ij).

Если множество вершин графа разбить на два непересекающихся подмножества, одно из которых содержит вершину-исток, а другое - вершину-сток, то множество дуг, соединяющих эти два множества, формируют разрез А, пропускная способность которого равна сумме пропускных способностей дуг. Таких разрезов может быть несколько.

Например, для А₁ имеем Х’={x₀} и X\Х’={х_i, х_j, х_k}, для А₂: Х’={х₀, х_i} и X\Х’={х_j, х_k}, для А₃: Х’={х₀, х_i, x_j} и X\Х’={х_k}, для А₄: Х’={х₀, х_j} и X\Х’={x_i, х_k}.       Очевидно, что величина максимального потока ограничена минимальной пропускной способностью разреза, т.е. j_max=min{с_Ai}.

Итак, максимальный поток в сети с заданными пропускными способностями дуг графа можно находить, вычисляя пропускные способности всех дуг и выбирая среди них - минимальное. Однако при таком решении задачи остается неизвестным распределение потока по дугам графа.