Математика \ Дискретная математика

Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 14

и сформировать фрагмент G’=<X’; r’`>, включив вторую концевую вершину в подмножество Х’;

шаг3: выбрать ребро минимального веса, смежное вершинам фрагмента и не являющееся петлей: а) если вторая концевая вершина не принадлежит фрагменту,

то включить ее в подмножество Х’,  ребро включить в фрагмент остова G’=<X’; r’`>, б) если вторая концевая вершина принадлежит фрагменту, то исключить данное ребро из анализа;

шаг 4: если все вершины графа вошли во фрагмент остова, т.е. Х'=Х, то конец, иначе перейти к шагу 2.

Пример: Постоить для графа (рис. 29а)) остов по алгоритму Дейкстра, приняв начальной вершиной x0 (рис.29b).


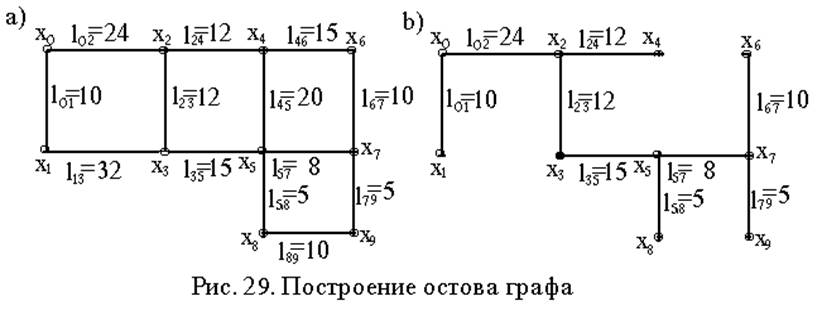 Результаты поэтапного построения остова графа приведены в таблице.

 Максимальный вес минимального остова графа по алгоритму Дейкстра равен

 L=Slij = (10+24+12+12+15+5+8+5+10=101.

ш

а

г

ребра, включаемые в остов

вершины, включаемые в остов

l01

l02

l23

l24

l35

l58

l57

l79

l67

x0

x1

x2

x3

x4

x5

x8

x7

x9

x6

1

1

0

0

0

0

0

0

0

0

1

1

0

0

0

0

0

0

0

0

2

1

1

0

0

0

0

0

0

0

1

1

1

0

0

0

0

0

0

0

3

1

1

1

0

0

0

0

0

0

1

1

1

1

0

0

0

0

0

0

4

1

1

1

1

0

0

0

0

0

1

1

1

1

1

0

0

0

0

0

5

1

1

1

1

1

0

0

0

0

1

1

1

1

1

1

0

0

0

0

6

1

1

1

1

1

1

0

0

0

1

1

1

1

1

1

1

0

0

0

7

1

1

1

1

1

1

1

0

0

1

1

1

1

1

1

1

1

0

0

8

1

1

1

1

1

1

1

1

0

1

1

1

1

1

1

1

1

1

0

9

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

1

lij

10

24

12

12

15

5

8

5

10

L=10+24+12+12+15+5+8+5+10=101.

По алгоритму Краскала:

шаг 1: установить частичный порядок по весу ребер графа;

шаг2: выбрать ребро минимального веса, не являющееся петлей, сформировать фрагмент остова G’=<X’; r’`>, а концевые вершины ребра включить в подмножество Х’ÍХ;

шаг3: выбрать ребро минимального веса, не являющееся петлей и не принадлежащее фрагменту: а) если фрагменту принадлежит одна вершина ребра, то вторую концевую вершину включить в подмножество Х’,  ребро включить в фрагмент остова G’=<X’; r’`>, б) если ни одна концевая вершина ребра не принадлежит фрагменту остова, то сформировать фрагмент другого остова, в) если концевые вершины принадлежат различным остовам, то соединить фрагменты;

шаг 4: если все вершины графа вошли во фрагмент остова, то конец, иначе перейти к шагу 2.

Пример: Постоить для графа (рис. 29а)) остов по алгоритму Краскала (рис. 29b).

Скачать файл