Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 6

3. 2 Числа графа

Функции, заданные на множестве графов {G=<X; r>} и принимающие значения на множестве целых чисел, называют числовыми характеристиками графа или просто числами. Наиболее очевидными и простыми числами являются: число вершин - n, число рёбер - m, степени вершин - d_i(или d_i⁺/d_i^-). Остальные числа графа требуют вычисления их значений.

Число компонент связности графа G=<X; r>. Если множество вершин графа G можно разбить на попарно непересекающиеся непустые подмножества X={X₁’;X₂’;…;X_k’} так, чтобы никакие две вершины из разных подмножеств не были смежны, то подграфы G₁=<X₁’;r₁’>,  G₂=<X₂’;r₂’>,…, G_k=<X_k’;r_k’> являются связными, а их число называют числом компонент связности графа G и обозначают k(G). Поиск числа компонент связности графа есть результат решения системы соотношений: если X_iÈX_j¢=X и  X_i¢ÇX_j¢=Æ для i¹j, 1£i, j£k, то  существуют графы, для которых G_iÈG_j=G и G_iÇG_j=Æ для i¹j, 1£i,j£k . Для поиска числа компонент связности используют механизм вычисления матриц достижимости (см. 3.3) и определения полных подграфов.

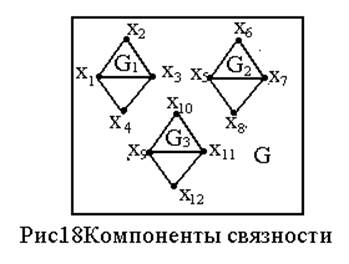
На рис. 18 дан граф, содержащий три компоненты графа G=<X; r>, где

X={x₁, x₂, x₃, x₄, x₅, x₆, x₇, x₈, x₉, x₁₀, x₁₁}, G₁=<X₁; r₁>, где X₁={x₁, x₂, x₃, x₄},

G₂=<X₂; r₂>, где X₂={x₅, x₆, x₇, x₈}, G₃=<X₃; r₃>, где X₃={x₉, x₁₀, x₁₁}.

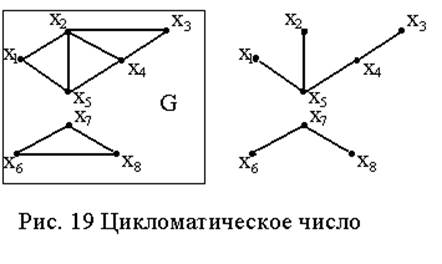Цикломатическое число графа G=<X; r>. Наименьшее число рёбер, удаление которых приводит к графу без циклов и петель, называют цикломатическим числом и обозначают l(G).

Цикломатическое число можно определить по формуле l(G)=m-n+k(G),

где m - число рёбер, n - число вершин, k(G) - число компонент связности графа. Для графа на рис. 19 имеем n=8, m=10, k(G)=2 и l(G)=10-8+2=4.

Cледовательно, для устранения циклов в данном графе нужно удалить минимум четыре ребра. Например,  {(x₁, x₂), (x₂, x₃), (x₂, x₄), (x₆, x₈)} или    {(x₁, x₅), (x₄, x₅),

(x₃, x₄), (x₆, x₇)}.

Хроматическое число графаG=<X;r>. Раскраской вершин графа в g цветов называют разбиение множества вершин связного графа на попарно непересекающиеся непустые подмножества, состоящие из попарно несмежных вершин, т.е. X_i ÈX_j¢=X и X_i¢ÇX_j¢=Æ, для i¹j, 1 £i, j £g.

Тогда каждому подмножеству X_i можно соотнести особый цвет краски. В этом случае никакие две смежные вершины не могут быть окрашены в один цвет.Наименьшее число g, при котором никакие две смежные вершины графа не могут быть окрашены в один цвет, называют хроматическим числом графа.

Нахождение хроматического числа достаточно трудоёмкая задача. Однако, можно дать оценку этого числа. Так хроматическое число полного n-вершинного графа равно n, пустого графа - 1, графа с циклом чётной длины - 2, графа с циклом нечётной длины - 3, графа типа дерево - 2. В отдельных случаях может быть рекомендована оценка по следующей формуле: g£max_i{d_i+1}. Например, для графа на рис. 12а) g=5, на рис. 12b) r=1, на рис. 13а) g=2, на рис. 20  g=4.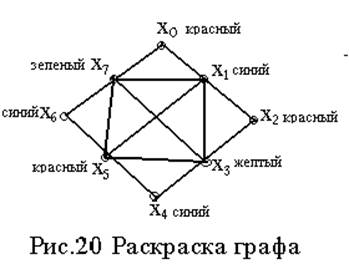

Плотность графаG=<X; r>. Наибольшее число вершин полного подграфа G¢=<X¢; r¢> связного графа G=<X; r>, между всеми вершинами которого задано отношение смежности, называют плотностью графа G и обозначают r(G), т.е.

r(G)= max_i{|X¢_i|}.

Например, для графа на рис. 13a)  r=5, на рис. 20 r=4 и т. д.

Механизм вычисления плотности приведен в 3.3.

Неплотность графаG=<X;r>. Наибольшее число вершин пустого подграфа G¢=<X¢;r¢> связного графа G=<X; r>, между всеми вершинами которого нет смежности, называют неплотностью графа G и обозначают e(G), т.е.: