Математика \ Дискретная математика

Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 17

шаг 4: сравнить каждый невычеркнутый элемент lijp с суммой (li,p+ lp,j)p для формирования значений li,j и ni,j  на очередном шаге итерации:

a) если (li,p+ lp,j)p<li,jp, то li,jp+1=(li,p+ lp,j)p, а ni,j (p+1)=p;

b) если (li,p+ lp,j)p>li,jp, то li,jp+1=li,jp; ni,j (p+1)= ni,j p.

шаг 5: если p<n, то принять p=p+1 и вернуться к шагу 4, иначе конец.


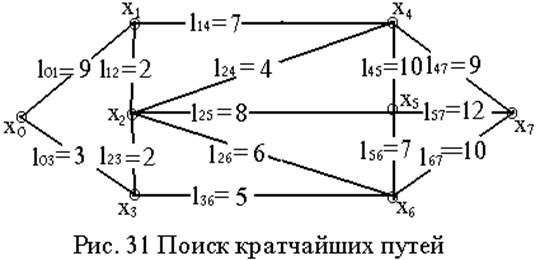Пример: Найти кратчайшие пути между вершинами графа (см. рис. 31).

Ниже таблицами показан процесс вычисления от p=0 до p=7

l0

x0

x1

x2

x3

x4

x5

x6

x7

n0

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

9

∞

3

∞

∞

∞

∞

x0

x0

x1

x2

x3

x4

x5

x6

x7

x1

9

0

2

∞

7

∞

∞

∞

x1

x0

x1

x2

x3

x4

x5

x6

x7

x2

∞

2

0

2

4

8

6

∞

x2

x0

x1

x2

x3

x4

x5

x6

x7

x3

3

∞

2

0

∞

∞

5

∞

x3

x0

x1

x2

x3

x4

x5

x6

x7

x4

∞

7

4

∞

0

10

∞

9

x4

x0

x1

x2

x3

x4

x5

x6

x7

x5

∞

∞

8

∞

10

0

7

12

x5

x0

x1

x2

x3

x4

x5

x6

x7

x6

∞

∞

6

5

∞

7

0

10

x6

x0

x1

x2

x3

x4

x5

x6

x7

x7

∞

∞

∞

∞

9

12

10

0

x7

x0

x1

x2

x3

x4

x5

x6

x7

l1

x0

x1

x2

x3

x4

x5

x6

x7

n1

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

9

∞

3

∞

∞

∞

∞

x0

x0

x1

x2

x3

x4

x5

x6

x7

x1

9

0

2

12

7

∞

∞

∞

x1

x0

x1

x2

x0

x4

x5

x6

x7

x2

∞

2

0

2

4

8

6

∞

x2

x0

x1

x2

x3

x4

x5

x6

x7

x3

3

12

2

0

∞

∞

5

∞

x3

x0

x0

x2

x3

x4

x5

x6

x7

x4

∞

7

4

∞

0

10

∞

9

x4

x0

x1

x2

x3

x4

x5

x6

x7

x5

∞

∞

8

∞

10

0

7

12

x5

x0

x1

x2

x3

x4

x5

x6

x7

x6

∞

∞

6

5

∞

7

0

10

x6

x0

x1

x2

x3

x4

x5

x6

x7

x7

∞

∞

∞

∞

9

12

10

0

x7

x0

x1

x2

x3

x4

x5

x6

x7

l2

x0

x1

x2

x3

x4

x5

x6

x7

n2

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

9

11

3

16

∞

∞

∞

x0

x0

x1

x1

x3

x1

x5

x6

x7

x1

9

0

2

12

7

∞

∞

∞

x1

x0

x1

x2

x0

x4

x5

x6

x7

x2

11

2

0

2

4

8

6

∞

x2

x1

x1

x2

x3

x4

x5

x6

x7

x3

3

12

2

0

19

∞

5

∞

x3

x0

x0

x2

x3

x1

x5

x6

x7

x4

16

7

4

19

0

10

∞

9

x4

x1

x1

x2

x1

x4

x5

x6

x7

x5

∞

∞

8

∞

10

0

7

12

x5

x0

x1

x2

x3

x4

x5

x6

x7

x6

∞

∞

6

5

∞

7

0

10

x6

x0

x1

x2

x3

x4

x5

x6

x7

x7

∞

∞

∞

∞

9

12

10

0

x7

x0

x1

x2

x3

x4

x5

x6

x7

l3

x0

x1

x2

x3

x4

x5

x6

x7

n3

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

9

11

3

15

19

17

∞

x0

x0

x1

x1

x3

x2

x2

x2

x7

x1

9

0

2

4

6

10

8

∞

x1

x0

x1

x2

x2

x2

x2

x2

x7

x2

11

2

0

2

4

8

6

∞

x2

x1

x1

x2

x3

x4

x5

x6

x7

x3

3

4

2

0

6

10

5

∞

x3

x0

x2

x2

x3

x2

x2

x6

x7

x4

15

6

4

6

0

10

10

9

x4

x2

x2

x2

x2

x4

x5

x2

x7

x5

19

10

8

10

10

0

7

12

x5

x2

x2

x2

x2

x4

x5

x6

x7

x6

17

8

6

5

10

7

0

10

x6

x2

x2

x2

x3

x2

x5

x6

x7

x7

∞

∞

∞

∞

9

12

10

0

x7

x0

x1

x2

x3

x4

x5

x6

x7

l4

x0

x1

x2

x3

x4

x5

x6

x7

n4

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

7

5

3

9

13

8

∞

x0

x0

x3

x3

x3

x3

x3

x3

x7

x1

7

0

2

4

6

10

8

∞

x1

x3

x1

x2

x2

x2

x2

x2

x7

x2

5

2

0

2

4

8

6

∞

x2

x3

x1

x2

x3

x4

x5

x6

x7

x3

3

4

2

0

6

10

5

∞

x3

x0

x2

x2

x3

x2

x2

x6

x7

x4

9

6

4

6

0

10

10

9

x4

x3

x2

x2

x2

x4

x5

x2

x7

x5

13

10

8

10

10

0

7

12

x5

x3

x2

x2

x2

x4

x5

x6

x7

x6

8

8

6

5

10

7

0

10

x6

x3

x2

x2

x3

x2

x5

x6

x7

x7

∞

∞

∞

∞

9

12

10

0

x7

x0

x1

x2

x3

x4

x5

x6

x7

l5

x0

x1

x2

x3

x4

x5

x6

x7

n5

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

7

5

3

9

13

8

18

x0

x0

x3

x3

x3

x3

x3

x3

x4

x1

7

0

2

4

6

10

8

15

x1

x3

x1

x2

x2

x2

x2

x2

x4

x2

5

2

0

2

4

8

6

13

x2

x3

x1

x2

x3

x4

x5

x6

x4

x3

3

4

2

0

6

10

5

15

x3

x0

x2

x2

x3

x2

x2

x6

x4

x4

9

6

4

6

0

10

10

9

x4

x3

x2

x2

x2

x4

x5

x2

x7

x5

13

10

8

10

10

0

7

12

x5

x3

x2

x2

x2

x4

x5

x6

x7

x6

8

8

6

5

10

7

0

10

x6

x3

x2

x2

x3

x2

x5

x6

x7

x7

18

15

13

15

9

12

10

0

x7

x4

x4

x4

x4

x4

x5

x6

x7

l6

x0

x1

x2

x3

x4

x5

x6

x7

n6

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

7

5

3

9

13

8

18

x0

x0

x3

x3

x3

x3

x3

x3

x4

x1

7

0

2

4

6

10

8

15

x1

x3

x1

x2

x2

x2

x2

x2

x4

x2

5

2

0

2

4

8

6

13

x2

x3

x1

x2

x3

x4

x5

x6

x4

x3

3

4

2

0

6

10

5

15

x3

x0

x2

x2

x3

x2

x2

x6

x4

x4

9

6

4

6

0

10

10

9

x4

x3

x2

x2

x2

x4

x5

x2

x7

x5

13

10

8

10

10

0

7

12

x5

x3

x2

x2

x2

x4

x5

x6

x7

x6

8

8

6

5

10

7

0

10

x6

x3

x2

x2

x3

x2

x5

x6

x7

x7

18

15

13

15

9

12

10

0

x7

x4

x4

x4

x4

x4

x5

x6

x7

l7

x0

x1

x2

x3

x4

x5

x6

x7

n7

x0

x1

x2

x3

x4

x5

x6

x7

x0

0

7

5

3

9

13

8

18

x0

x0

x3

x3

x3

x3

x3

x3

x4

x1

7

0

2

4

6

10

8

15

x1

x3

x1

x2

x2

x2

x2

x2

x4

x2

5

2

0

2

4

8

6

13

x2

x3

x1

x2

x3

x4

x5

x6

x4

x3

3

4

2

0

6

10

5

15

x3

x0

x2

x2

x3

x2

x2

x6

x4

x4

9

6

4

6

0

10

10

9

x4

x3

x2

x2

x2

x4

x5

x2

x7

x5

13

10

8

10

10

0

7

12

x5

x3

x2

x2

x2

x4

x5

x6

x7

x6

8

8

6

5

10

7

0

10

x6

x3

x2

x2

x3

x2

x5

x6

x7

x7

18

15

13

15

9

12

10

0

x7

x4

x4

x4

x4

x4

x5

x6

x7
Скачать файл