Пример: На рис.22 дан граф. Определить его внешнюю устойчивость.
Сформируем, как и для внутренней устойчивости, списки смежных (hxi) и несмежных (ùhxi) вершин (см. табл. a) предыдущего примера).
Так как в табл. a) есть несмежные вершины, то сформируем подмножества всех вершин графа {xi, xj}ÍX и списки смежныx (hxi,xj) и несмежныx (ùhxi,xj) им вершин (см. табл. d). Анализ табл. d) показывает, что существуют двухэлементные подмножества, смежные со всеми оставшимися вершинами графа G.
табл. d) продолжение табл. d)
|
{xi, xj} |
h{xi, xj} |
ùh{xi, xj} |
{xi, xj} |
h{xi, xj} |
ùh{xi, xj} |
|
|
x1, x2 |
x3, x4, x5 |
x6, x7 |
x3, x4 |
x1, x2, x5, x6 |
x7 |
|
|
x1, x3 |
x2, x4, x5, x6 |
x7 |
x3, x5 |
x1, x2, x4, x6, x7 |
Æ |
|
|
x1, x4 |
x2, x3, x6 |
x5, x7 |
x3, x6 |
x1, x2, x4, x5, x7 |
Æ |
|
|
x1, x5 |
x2, x3, x4, x7 |
x6 |
x3, x7 |
x1, x2, x4, x5, x6 |
Æ |
|
|
x1, x6 |
x2, x3, x4, x7 |
X5 |
x4, x5 |
x1, x2, x3, x6, x7 |
Æ |
|
|
x1, x7 |
x2, x3, x4, x5, x6 |
Æ |
x4, x6 |
x1, x4, x7 |
x2, x5 |
|
|
x2, x3 |
x1, x4, x5, x6 |
x7 |
x4, x7 |
x1, x3, x5, x6 |
x2 |
|
|
x2, x4 |
x1, x3, x5, x6 |
x7 |
x5, x6 |
x2, x3, x4, x7 |
x1 |
|
|
x2, x5 |
x1, x3, x7 |
x4, x6 |
x5, x7 |
x2, x3, x6 |
x1, x4 |
|
|
x2, x6 |
x1, x3, x4, x5, x7 |
Æ |
x6, x7 |
x3, x4, x5 |
x1, x2 |
|
|
x2, x7 |
x1, x3, x5, x6 |
x4 |
Следовательно, множества, содержащие наименьшее число вершин, смежных с оставшимися вершинами графа, есть T={{x1, x7}; {x2, x6}; {x3, x5}; {x3, x6}; {x3, x7}; {x4, x5}}, т. е. число внешней устойчивости графа f(G)=mini{|Ti|}=2.
3.3.2. Бинарные операции.
При исполнении операций над двумя графами G1=<X1; r1> и G2=<X2; r2> следует обратить внимание на наличие общих элементов для X1 и X2 и/или r1 и r2. Этот анализ позволяет выделить три конструктивных объекта:
1. вершины и рёбра (дуги) не имеют общих элементов, т.е. (X1ÇX2)=Æ и (r1Çr2)=Æ;
2. вершины имеют общие элементы, а рёбра (дуги) - нет, т.е. (X1ÇX2)¹Æ и (r1Çr2)=Æ;
3. вершины и рёбра (дуги) имеют общие элементы, т.е. (X1ÇX2)¹Æ и (r1Çr2)¹Æ.
Исполнение операций для каждого из них порождает принципиально иной объект.
Объединение графов G1=<X1; r1> и G2=<X2; r2> есть граф G=G1ÈG2), для которого X=(X1ÈX2) и r=(r1Èr2). рис. 23 дан результат этой операции. Для вычисления смежности вер- шин формируемого графа следует использовать матрицы смежности по формуле: ri,j=ri,j(1)Ú ri,j(2). Матрица смежности для графа G=<X; r> будет иметь число строк и столбцов равным |X|=|X1|+|X2|.
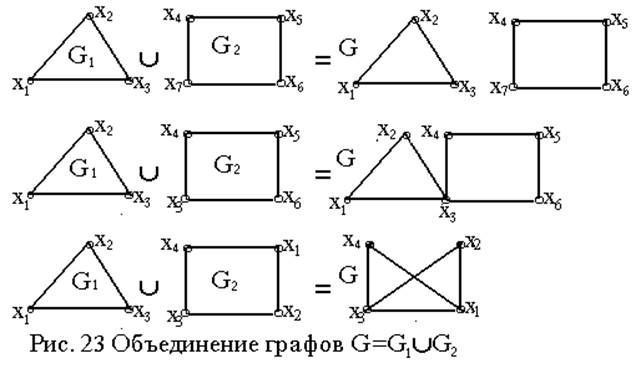 |
Пересечение графовG1=<X1; r1> и G2=<X2; r2> есть граф G=(G1ÇG2), для которого X=(X1ÇX2) и r=(r1Çr2). На рис. 24 дан результат исполнения этой операции. Матрица смежности графа имеет число строк и столбцов равным |X|=|X1ÇX2|. Для вычисления смежности вершин формируемого графа следует воспользоваться формулой: ri,j=ri,j(1)× ri,j(2).
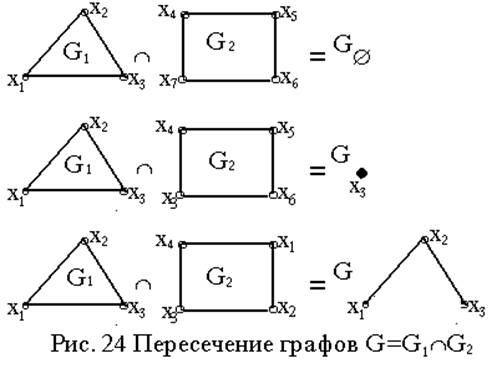 |
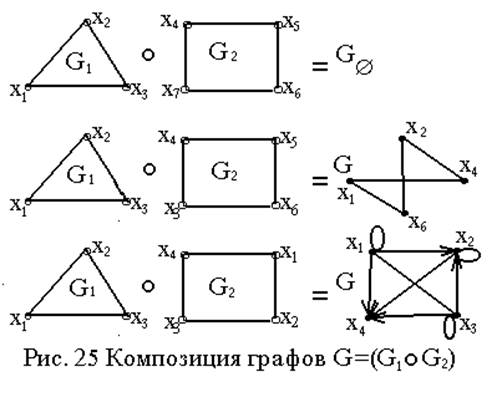 |
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.