Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 21

2) координировать исполнение работ всеми соисполнителями в заданные сроки и при заданном ресурсном обеспечении;

3) устанавливать последовательность и сроки использования ограниченных ресурсов в течение всего времени исполнения проекта;

4) выполнять анализ компромиссных решений по затратам и срокам выполнения работ с учетом резерва времени;

Каждый проект имеет перечень работ, продолжительность исполнения каждой работы, взаимосвязь и последовательность их исполнения.

Граф типа сеть является идеальным образом исполнения проекта. В этом графе только одна вершина-исток, она определяет начало работ по проекту, только одна вершина-сток, она определяет окончание исполнения проекта. Между вершинами истоком и стоком есть множество вершин-событий, фиксирующих начало и окончание каждой работы или комплекса  работ (t_i). Множество дуг, связывающих вершины-события, есть работы. Длина дуги-работы характеризует затраты временных, трудовых или финансовых ресурсов (t_ij). Комплекс работ отображается  на графе несколькими заходящими или исходящими дугами для одной вершины-события. В сетевом графе не должно быть петель и контуров. 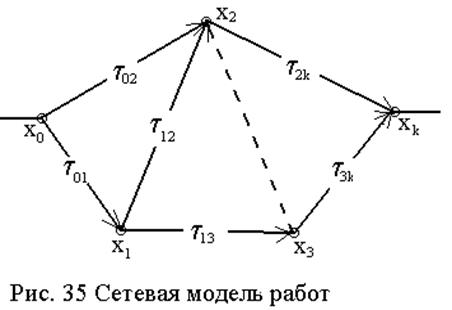Если две или несколько работ должны начинаться одновременно, но привязаны к различным вершинам-событиям, то между вершинами-событиями начала этих работ должна быть показана пунктирная линия, показывающая фиктивную работу – ожидание. Рассмотрим фрагмент графа (см. рис. 35), включающий в себя пять вершин-событий и шесть дуг-работ. х₀ - вершина-исток, определяющая начало работ по проекту в момент времени t₀, х_k – вершина-сток, определяющая окончание работ по проекту в момент времени t_k, t₀₁ и t₀₂- дуги-работы, которые могут быть начаты в момент t₀. Вершина-событие х₁ характеризует окончание работы t₀₁ в момент времени t₁=t₀+t₀₁и определяет  начало комплекса работ t₁₂ и t₁₃. Вершина-событие х₂ есть окончание работ t₀₂ и  t₁₂ в моменты времени t₂’=t₀+t₀₂ и t₂”=t₁+t₁₂ и определяет  начало последующей работы - t_2k по значению t₂=max{t₂’, t₂”}. Вершина-событие х₃ есть окончание работы t₁₃ в момент времени t₃=t₁+t₁₃ и определяет  возможность начать работы t_3k. Так как работы t_2k и t_3k должна начаться одновременно (см. пунктирную линию - ожидание), то следует найти максимальное значение t_ожид.= max{t₂, t₃}. Работы  t_2k и t_3k обеспечивают завершение проекта к моменту времени t_k=max{t_ожид.+t_2k, t_ожид.+t_3k}. Итак, наибольшая продолжительность работ по проекту есть максимальное значение t_k.

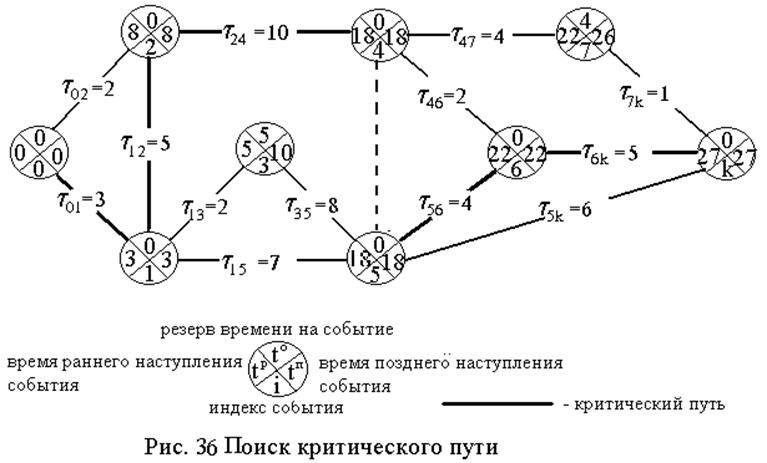
При наличии нескольких дуг-работ, заходящих в вершину-событие следует определять для каждого события сети ранний момент его наступления t^p(x_i), как наибольшее позднее окончание предшествующих работ, т. е. t^p(x_i)=max{(t^p(x_j)+t_i,j)}.

 При наличии нескольких дуг-работ, исходящих из вершины-события следует определять для каждого события сети поздний момент его наступления t^п(x_i), как наименьшее раннее окончание последующих работ, т. е. t^п(x_i)=min{(t^п(x_j)-t_i,j)}.

  Расчет ранних моментов наступления события следует начинать с x₀, а поздних моментов наступления события с x_k. Для событий, связанных с ожиданием ранний и поздний моменты времени расчитываются по формулам:

t^p_ожид^.(х_i;х_j)=max{t^p(х_i); t^p(х_j)}, tⁿ_ожид^.(х_i;х_j)=min{tⁿ(х_i); tⁿ(х_j)}.

Максимально время, на которое можно задержать наступление некоторого события без задержки срока завершения всего проекта, называют резервом времени события, т. е. t⁰(х_i)=tⁿ(х_i) - t^p(х_i). Если t⁰(x_i)=0, то задержка наступления этого события не допускается. Событие с нулевым резервом времени находятся на критическом пути сетевой модели проекта. Критический путь представляет собой последовательность работ и событий, имеющих нулевой резерв времени. Поэтому на критическом пути должно быть t⁰(x_i)=0 и t⁰_i,j=(tⁿ(х_j)- t^p(х_i)-t_i,j)=0. Величину t⁰_i,j=(tⁿ(х_j)- t^p(х_i)-t_i,j)³0 называют полным резервом времени на работу (i,j).

Для компактного изображения всех показателей каждого события каждую вершину-событие представим в виде круга, разбитого на четыре сектора. В каждом секторе указаны четыре показателя: индекс вершины (i), ранний момент наступления события t_p(x_i), поздний момент наступления события t_n(x_i) и резерв времени на событие t⁰(x_i). Дуги графа изображают работы, а пунктирная линия – фиктивную работу- ожидание. Для иллюстрации возможностей сетевого управления работами по проекту рассмотрим сетевую модель (см. рис. 36).