Последовательность смежных вершин, соединяющего вершины xi и xj , называют переходом и обозначают nij=(xi,..xj). Например, для неориентированного графа, приведенного на рис. 10, между вершинами x0 и x5 существует шесть переходов, т.е. n05={(x0, x4, x5); (x0, x1, x4, x5); (x0, x1, x5); (x0, x4, x1, x5); (x0, x4, x1, x3, x5);
(x0, x1, x3, x5)}.
Маршрут неориентированного графа, связывающий вершины xi и xj различными ребрами, называют цепью, а ориентированного - путём.
Маршрут называют простым, если при его обходе каждая промежуточная вершина встречается не более одного раза.
Маршрут называют открытым, если его концевые вершины различны, и замкнутым, если его концевые вершины совпадают. Замкнутый маршрут, который содержит только одно ребро или дугу, называют петлёй. На рис. 10 петля указана для вершины x4. Замкнутый маршрут называют циклом, замкнутый простой маршрут простым циклом.
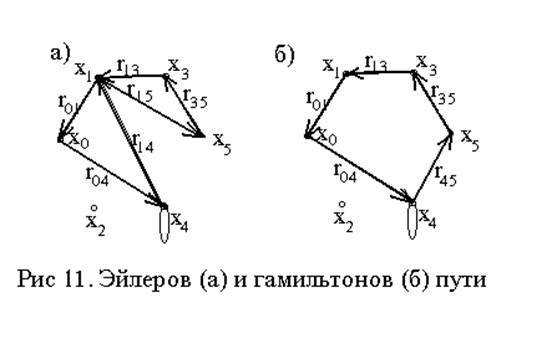
Маршрут называют эйлеровым, если он замкнут и проходит через каждое ребро графа только по одному разу. Таким является маршрут m00=(r04, r41, r15, r53, r31, r10)}, показанный на рис. 11.
 |
Длина маршрута равна числу смежных рёбер, соединяющих вершины xi и xj , т.е. li;j=Srk,l, где k¹l и i£k,l£j.
Длину минимального маршрута, соединяющего вершины xi и xj называют расстоянием. Например, расстояние между вершинами x0 и x5 графа, приведённого на рис. 10б), равно 2.
Если ребро или дуга обладают дополнительной характеристикой – протяжённостью - lk,l, то длина маршрута равна сумме длин рёбер или дуг, его составляющих, т.е. li;j=Sk,l, где k¹l и i£k,l£j.
Если ребро или дуга обладают дополнительной характеристикой - пропускной способностью - сk,l, то пропускная способность маршрута равна минимальной пропускной способности рёбер или дуг, его составляющих.
Граф называют связным, если любые две его вершины можно соединить цепью. Для ориентированного графа выделяют сильную связность, когда любые две его вершины взаимодостижимы при наличии дуг, и слабую связность, когда любые две его вершины достижимы только при условии замены дуг на рёбра.
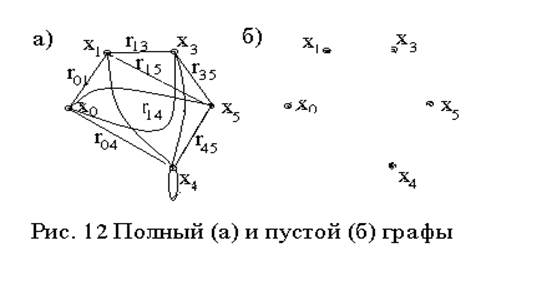 |
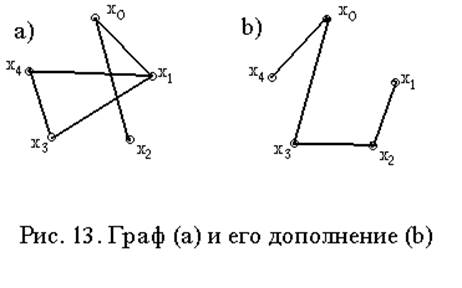
Граф называют дополнительным для графа G=<X; r>, если он опирается на множество вершин X и дополнения отношения r, т. е. ùG=<X;`r>.
Для формирования дополнительного графа G¢=ùG=<X; `r > необходимо найти дополнение отношения r по матрице смежности графа G:
![]() 1, если ri,j=0;
1, если ri,j=0;
 |
 Граф называют деревом, если он
связный, но без циклов, петель и кратных рёбер или дуг. Ориентированные деревья
интенсивно используют для представления в компьютере данных и организации
доступа к ним по ключу, для рганизации структуры программы и структуры
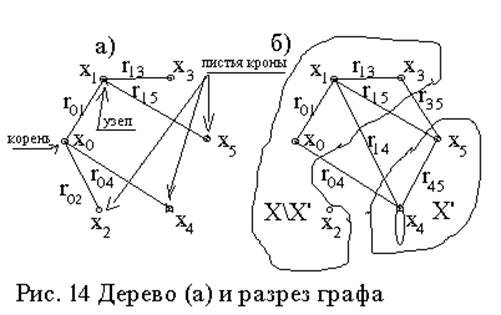
операторов управления, каталогов и файлов в операционных системах. В графе типа дерево (см. рис. 14а) всегда выделяют корневую
вершину, узлы и крону. Число рёбер или дуг графа равно (n-1), где n - число
вершин графа.
Граф называют деревом, если он
связный, но без циклов, петель и кратных рёбер или дуг. Ориентированные деревья
интенсивно используют для представления в компьютере данных и организации
доступа к ним по ключу, для рганизации структуры программы и структуры
операторов управления, каталогов и файлов в операционных системах. В графе типа дерево (см. рис. 14а) всегда выделяют корневую
вершину, узлы и крону. Число рёбер или дуг графа равно (n-1), где n - число
вершин графа.
Если множество вершин графа G=<X; r> разбить на два подмножества X’ и X\X’ при условии, что X’È(X\X’)=X и X’Ç(X\X’)=Æ, то множество рёбер или дуг, одни из концевых вершин которых принадлежат множеству X’, а другие - множеству (X\X’), называют разрезом. Поиск разрезов сводится к определению отношения принадлежности xiÎX’ и xjÎ(X\X’) с последующим выделению множества рёбер, соединяющих эти подмножества.
На рис. 14б) дан разрез {r04, r14, r15, r35}, cоединяющий два подмножества X’={x0, x1, x3} и (X\X’)={x4, x5}.
Удаление множества рёбер или дуг разреза преобразует связный граф в несвязный.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.