Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 12

Матрица смежности графа имеет число строк и столбцов |X|£|X₁ÈX₂|.

Изоморфизм графов G₁=<X₁; r₁> и G₂=<X₂; r₂>. Поскольку графы могут быть заданы различными способами, то трудно определить: одинаковы ли (изоморфны ли) графы.

Пусть даны два графа G₁=<X₁; r₁> и G₂=<X₂; r₂> и даны операторы  отображения множества вершин и рёбер одного графа на другой, т. е.

f₁: X₁®X₂, f₂: r₁®r₂ и

f₁^-1:X₂®X₁, f₂^-1: r₂ ®r₁.

Граф G₁ гомоморфен графу G₂ тогда и только тогда, когда вершина x_i⁽¹⁾ÎX₁ и инцидентное ему ребро r_i,j⁽¹⁾Îr₁ имеют отображение на графе G₂ в виде вершины f₁(x_i⁽¹⁾)=x₂ÎX₂ и инцидентного ребра f₂(r_i,j⁽¹⁾)=r_l,m⁽²⁾Îr₂. И наоборот, граф G₂ гомоморфен графу G₁ тогда и только тогда, когда вершина x_i⁽²⁾ÎX₂ и инцидентное ему ребро r_i,j⁽²⁾Îr₂ имеют отображение на графе G₁ в виде вершины f₁^-1 (x_i⁽²⁾)=x₁ÎX₁ и инцидентного ребра f₂^-1(r_i,j⁽²⁾)=r_l,m⁽¹⁾Îr₁.

Если существует прямой и обратный гомоморфизмы, то графы изоморфны.

 Необходимыми условиями изоморфизма являются равенство числа вершин и рёбер, одинаковость числа петель и набора степеней вершин графов, а достаточными - одинаковость матриц инциденции или смежности графов. На рис. 26 дан пример изоморфных графов.

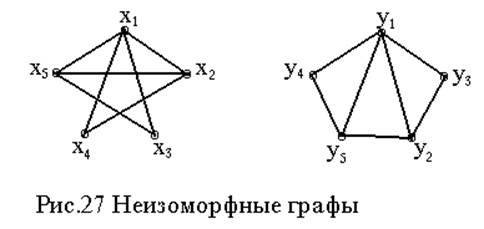
На рис. 27 приведены неизоморфные графы, хотя оба графа имеют одинаковое общее число вершин и ребер, число вершин с одинаковой валентностью, но различные матрицы ссмежности.

3.4. Некоторые алгоритмы на графах

3.4.1 Построение покрывающего остова