Дискретная математика: Учебное пособие. Часть 3 - Основы теории графов, страница 19

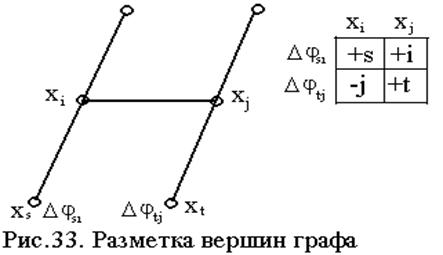
Для поиска распределения потока по дугам графа разработано несколько алгоритмов, особое место среди которых занимает алгоритм Форда-Фалкерсона, суть которого состоит в разметке вершин графа. Метка вершины графа указывает на возможность изменения потока через данную вершину и указывает источник этого изменения. На рис. 33 дан фрагмент сети, объясняющий суть алгоритма.

Если по дуге (х_s, х_i) возможно увеличение потока, т.е. j _si< c_si, то вершину х_i следует пометить +s  , что указывает на источник увеличения потока. Если по дуге (х_i, х_j) возможно увеличение потока j _ij< c_ij, то вершину х_j пометить +i . Это означает, что приращение потока  Dj_si пойдет по направлению дуги (х_i, х_j) от вершины х_s.

Если по дуге (х_t, х_j) возможно увеличение потока, т.е. j _tj< c_tj, то вершину х_j следует пометить +t , что указывает на источник увеличения потока. Однако, если вершина х_j не имеет пометки +i  , то для увеличения потока в фрагменте сети, следует уменьшить поток в дуге (х_i, х_j) и направить его далее по другим дугам фрагмента на сток. Для указания вершины, от которой необходимо уменьшить поток, ставят пометку –j  . Это означает что на участке (х_i, х_j) поток должен быть уменьшен на величину  Dj_tj.

Следует отметить, что вершины х_i и х_j могут иметь одновременно по нескольку подходящих и отходящих дуг. В примере, показанном на рис. 33 одновременно при допустимых  Dj _si и Dj _tj могут быть  для вершины х_j две метки +t   и   +i  для вершины х_i также две метки   +s   и   -j , что свидетельствует о свободе выбора приращения потока либо на величину Dj _si, либо  Dj _tj.

 Если дуга (х_s, х_i) насыщена, т.е. j _si=c_si, то метку  +s  у вершины х_i ставить нельзя. Если насыщена дуга (х_t, х_j), т.е. j _tj=c_tj, то метку  +t   у вершины х_j ставить нельзя.

Если вершина х_j не помечена, то нельзя ставить метку   -j   у вершины х_i. Когда обе вершины графа (х_i и х_j) не имеют меток, то это означает невозможность приращения потока. Так достигают максимального значения потока от вершин-истоков х_s и х_t по дугам к вершинам - стокам х_i и х_j.

Алгоритм Форда-Фалкерсона.

шаг 1: присвоить всем вершинам графа индексы 0,1,2,...k; где 0-индекс вершины-истока графа, k -индекс вершины-стока графа;

шаг 2: присвоить начальной вершине метку “0”;

шаг 3: все непомеченные вершины х_i, в которые идут ненасыщенные дуги из помеченной вершины х_s, пометить индексом “+s”, что свидетельствует о возможности увеличения потока из вершины х_s по дуге (х_s, х_i);

шаг 4: все непомеченные вершины х_i, из которых идут дуги (насыщенные или ненасыщенные) в помеченную вершину х_j, пометить индексом “-j”, что свидетельствует о возможности уменьшения потока в вершину х_j по дуге (х_i, х_j);

шаг 5: если в результате этих операций окажется помеченной вершина-сток x_k, то между начальной и конечной вершинами сети найдется маршрут, все вершины которого различны и с точностью до знака помечены индексами предыдущих вершин, формирующих переход, по которому можно увеличить поток, и перейти к шагу 6, иначе конец.

шаг 6: увеличить поток в маршруте, сформированном на шаге 5, на единицу и перейти к шагу 3.

Пример: На рис. 34 дан граф. Каждой дуге графа (х_i, х_j) приписаны величина потока и пропускная способность (j_ij,c_ij).  

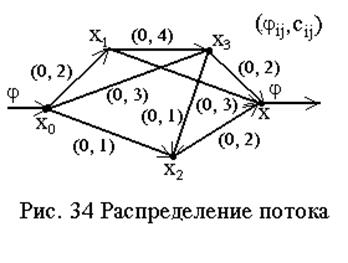Все расчеты по алгоритму сведены в две таблицы. В табл. а) на каждом шаге итерации для каждой вершины графа указаны возможные метки, а в табл. b) даны приращения потока по дугам (х_i;х_j). Символом “      “ в табл. b) показаны насыщенные дуги графа. В результате выполнения первого шага итерации возможны маршруты: n_0k={(х_k, х₁, х₀); (х_k, х₂, х₀); (х_k, х₂, х₃, х₀); (х_k, х₂, х₃, х₁, х₀); (х_k, х₃, х₀); (х_k, х₃, х₁, х₀)}, из множества которых был выбран маршрут m = (х_k, х₃, х₀).

                                                                                                    табл. а)