Методические указания к выполнению лабораторных работ с дисциплины "Основы расчета иконструирования машин и аппаратов пищевых производств", страница 17

где                           

m - угловой коэффициент, равный тангенсу угла, образованного прямой с положительным направлением оси абсцисс;

п - отрезок по оси ординат, соответствующий величине S , рав­ной 1 ( х = lgS = lg1 = 0).

Принимая n = lgc и подставляя соответ­ствующие величины в написанное уравнение прямой, получаем:

Протенцинируя, находим                    

написанная формула и будет искомой.

Главнейшим недостатком графического метода является некото­рая субъективность в проведении прямой линии, наиболее соответ­ствующей нанесенным на график опытным точкам.

От этого недостатка свободен аналитический метод, основанный на применении способа наименьших квадратов (метод Гаусса).

Положим, что требуется найти зависимость   на основании ряда величин Р_z , найденных опытным путем, при раз­личных значениях для S . Неизвестными в данном случае являются: коэффициент  с и показатель т. Логарифмируя написанное выражение, получаем:

                                                                      (14)

искомая формула будет удовлетворять фактически данным с известным приближением. Поэтому, подставляя в уравнение (14) фактически ве­личины, мы получим некоторые отношения и уравнению (14) будет соответствовать ряд неравенств:

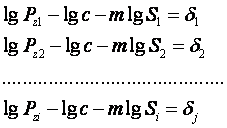                                                            (15)

где j - общее число наблюдений.

Согласно основному положению метода наименьших квадратов, искомые величины с и т могут быть найдены из условия, чтобы сумма квад­ратов отношений σ была минимальной, т.е. 

Это условие приводит к следующим уравнениям:

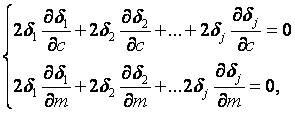                                              (16)

Используя уравнение (15), получаем:

написанные уравнения приводятся к следующим:

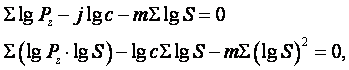                                                  (17)

Из двух уравнений с двумя неизвестными  lgc и m находятся интересующие величины. Под знаками суммы в уравнениях стоят ве­личины, непосредственно найденные из опытов.

Способ натянутой нити основан на геометрическом подборе пря­мой на глаз. Нанеся наблюдаемые значения на миллиметровку; графи­чески подбирается прямая, ближе всего подходящая к наблюдаемым точ­кам. Выбрав две произвольные точки на этой прямой, определяются их координаты x₁ у₁ x₂ у₂. Тогда для определения коэффициен­тов m и n получается для простых уравнения:

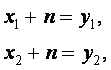                                                                                     (18)

Способ средней не требует графического изображения эксперименталь­ных данных и состояний в следующем. Пусть значения наблюдений даны в таблице 1.

Таблица I Данные наблюдений

х	х1	х2	х3	…	хn-1	хn
у	у1	у2	у 3	…	уn-1	уn