Методические указания к выполнению лабораторных работ с дисциплины "Основы расчета иконструирования машин и аппаратов пищевых производств", страница 16

1) установление общего вида искомой функциональной зависимос­ти;

2) вычисление оценок, входящих в это уравнение параметров.

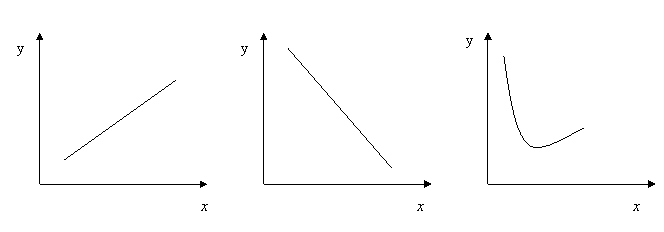
рис.2.

При выборе вида кривой следует сочетать исследование расположения опытных точек на графике с логическо-профессиональным анализом. Нанеся экспериментальные данные на график, получил корреляционное поле (рис. 2), характеризующее зависимость между исследуемыми переменными. Для этого, чтобы проследить основное напряжение вытянутости этого корреляционного поля, удобно ис­пользовать частные средние _i. По характеру расположения точек приближенно определяется характер зависимости (линейная, параболическая, гиперболическая и т.д.)

Вторая задача может быть сформулирована следующим образом: по данным эксперимента имеет массив пар х и у, не­обходимо найти уравнение приближенной регрессии с конкретны­ми значениями числовых коэффициентов и оценить допускаемую при этом ошибку. В дальнейшем уравнение приближенной регрессии за­писывается в виде у = f (х) понимая под этим, что у ≈ f (х).

Наибольшее распространение имеет линейная форма связи  между у и х, отображаемая уравнением вида

у= a + bх                                                                       (10)

 Линейную регрессию можно рассматривать как частный случай об­щей параболической зависимости, выражаемой

у=а+в₁х+в₂х + ….+в_n х                                                    (11)

При исследовании линейной регрессии вида  у= a + bх   необходимо найти неизвестные коэффициенты «а» и «в». Они опре­деляются с использованием метода наименьших квадратов. Сущность этого метода заключается в том, что наилучшая линия, рассеян­ных на плоскости ху , должна занимать положение, при кото­ром сумма квадратов отклонений точек от этой линии минимальна. Именно это правило и объясняет происхождение термина «метод наименьших квадратов».

Формулы для вычисления коэффициентов линейной регрессии:

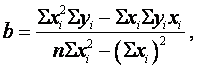                                                        (12)

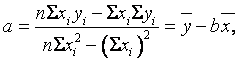                                                (13)

Определенная по формуле (12) величина называется коэффици­ентом регрессии у относительно х . Она характеризует угол накло­на прямой регрессии. Если «в» > 0, то с увеличением х значение у также возрастает, если  «в» < 0 - у убывает при возрастании х.

Качественной проверкой уравнения регрессии является проверка на адекватность, т.е. на соответствие управления действительности. Проверка на адекватность проводится с помощью специальных крите­риев, например, критерия Фишера. Но можно ограничиться эксперимен­тальной проверкой полученного уравнения, то есть подстановкой в него известных значений и сопоставлением полученных результатов с действительными. Если разница действительных и вычисленных значе­ний невелика, то данное уравнение оставляют и считают его вполне приемлемым и правильно отражающим связь.

3.5. Построение графиков

Результаты лабораторного исследования могут быть часто пред­ставлены степенными функциями. Нахождение этих функций произво­дится либо графически, либо аналитически.

В первом случае данные опытов наносятся на двойную логариф­мическую сетку, и если точки хорошо укладываются на одной прямой, то по углу наклона прямой к оси абсцисс и по отрезку, отсекаемому его на оси ординат, можно найти искомую зависимость.

Так, например, если отложить на оси абсцисс логарифм подач S, а по оси ординат логарифмы величин усилия резания Р_z , располо­жение опытных точек получается примерно вдоль прямой; тогда иско­мая зависимость Р_z = f(S) может быть найдена, исходя из урав­нения этой прямой   y = m x - n ,