Методические указания к выполнению лабораторных работ с дисциплины "Основы расчета иконструирования машин и аппаратов пищевых производств", страница 11

где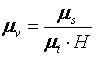                                                                

есть масштаб скорости диаграммы  v = f(t).

Перенеся отрезки 0 – I^”, 0 – 2”, 0 - 3" и т.д. на ординаты в соответствующих положениях, получим точки 0, 1’”, 2’”, 3”’ и т.д., соединив которые плавной кривой, получим диаграмму v = f(t).

Мы указывали, что отрезок Н выбирается произвольно. Чем больше Н, тем меньше масштаб скоростей μ_v  и тем больше величи­ны ординат диаграммы v = f(t). При выборе Н следует ориенти­роваться на наиболее крутую касательную. Правильный выбор вели­чины отрезка Н достигается опытом.

Кривая скорости является дифференциальной кривой по отноше­нию к диаграмме пути, и наоборот, график пути является интеграль­ной кривой по отношению к графику скоростей.

Из курса математического анализа известно, что:

а) максимальной и минимальной ординатам графика перемещения должны соответствовать ординаты, равные нулю на дифференциальном графике скоростей;

б) точке перегиба графика перемещений должны соответствовать максимальные или минимальные ординаты графика скоростей.

Это видно из сопоставления графиков S = f (t) и v = f(t) (см. рис. 13 ). Указанные положения следует также учитывать при графическом дифференцировании.

График ускорений можно получить, продифференцировав анало­гичным образом график скоростей. При этом, если траектория дви­жения точки является криволинейной, то полученные ускорения будут только касательными, если же движение точки является пря­молинейным, то ускорение будет полным.

Рис. 13 Графическое дифференцирование по методу касательных

Точное проведение касательных к кривой является затрудни­тельным. Поэтому графическое дифференцирование по методу каса­тельных недостаточно точно.

Метод хорд

Метод хорд заключается в следующем. Разбиваем кривую на ряд участков (участки могут быть неравными) и заменяем на этих участках кривые хордами (рис. 14а), т.е. неравномерное дви­жение на каждом участке приближенно заменяем движением равно­мерным с постоянной скоростью, равной действительной средней скорости на данном участке.

На оси t  будущей диаграммы v = f(t)  влево от начала координат на произвольном расстоянии Н выбираем точку 0' (рис. 14 б). Из этой точки проводим лучи 0'- 1", 0'- 2", 0'- 3" и т.д., параллельные соответствующим хордам 0-1', 1’- 2,' 2'- З' и т.д. Эти лучи отсекают на оси v отрезки 0-1", 0 – 2”, 0 - 3" и т.д., пропорциональные средним скоростям на соответст­вующих участках. Откладывая равные этим отрезкам ординаты z_i  на соответствующих участках, получим ступенчатую линию 1”-1’”,1’”- 2’”,2’”-З’” и т.д. графика скорости. Истинный график скорости легко получить, проведя плавную кривую через уступы ступенчато­го графика таким образом, чтобы площади заштрихованных площадок, расположенных с обеих сторон кривой на каждом участке, были одинаковы.

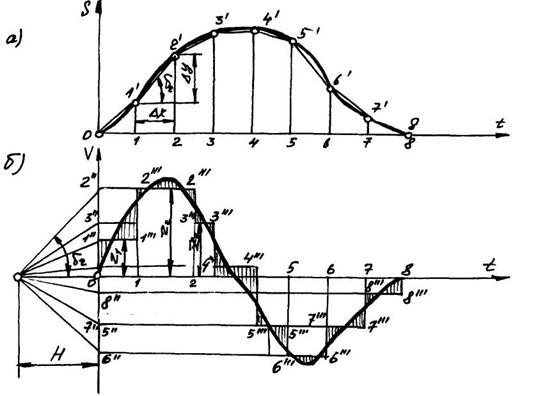
Рис. 14. Графическое дифференцирование по методу хорд

При проведении кривой v = f(t)  с достаточной для прак­тики точностью можно принять, что она проходит через середины уступов 1" – 1’", 2"’ – 2”', 3"' - 3'" и т.д. Это облегчает построе­ние кривой. Следует отметить, что при проведении хорд на графике S = f (t) нужно, чтобы эти хорды были достаточно близки к кривой. Если этого не получается, то участок следует разбить на более мелкие части. Например, на участке 1-2 (рис. 15 ) хорда ав в далека от кривой, поэтому участок нужно разбить на два меньших участка (1-1’и 1’-2) и на них к кривой провести две новые хорды aс и cв.