![]()
Для определения действительного искомого положения толкателя достаточно из точки 0’ провести прямую под углом ψ1 к линии центров 00’ (эта прямая на рисунке показана пунктиром).
1. После построения диаграммы перемещений проверить правильность ее построения экспериментально. Для этого для ряда произвольных положений кулачка, отмеченных сектором, определить индикатором или сектором соответствующие положения толкателя.
2. Построить диаграмму скорости путем графического дифференцирования диаграммы перемещений. Суть метода состоит в следующем:
Известно, что скорость является производной пути по времени
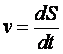
|
Рис, 11 . Определение положения качающегося плоского толкателя |
Поэтому, если задана диаграмма пути S = f (t), то методом графического дифференцирования можно определить скорость в любом положении.
На рис. 12 представлена диаграмма пути S = f (t). Определим скорость v в положении 1:
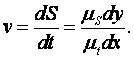
где dy- элементарный отрезок (мм), изображающий в масштабе μs элементарное перемещение dS;
dx- элементарный отрезок (мм), изображающий в масштабе μ t элементарное время dt.
Отношение ![]() , как это известно из математики,
есть тангенс угла наклона касательной к оси абсцисс. Обозначив этот угол через
δ, получим
, как это известно из математики,
есть тангенс угла наклона касательной к оси абсцисс. Обозначив этот угол через
δ, получим
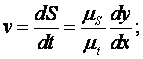
Тогда
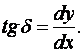
Таким образом, скорость в рассматриваемый момент времени пропорциональна тангенсу угла между касательной к кривой S = f (t) в соответствующей точке и осью t .
Формула является основной формулой при графическом дифференцировании.
Имеется несколько методов графического дифференцирования. Рассмотрим два из них: метод касательных и метод хорд.
Метод касательных
На рис. 13а представлена диаграмма S = f (t). В точках 0’, 1’ , 2' и т.д. проводим касательные к кривой S = f (t). На оси t будущей диаграммы v = f(t) влево от начала координат выберем точку 0’ на произвольном расстоянии Н от начала координат (рис. 13б). Через точку 0’ проводим лучи 0'- 1", 0’- 2", 0'- 3” и т.д., параллельные касательным в точках 1, 2, 3 и т.д. диаграммы S = f (t). Эти лучи отсекают на оси отрезки 0 – 1”, 0-2", 0 - 3" и т.д., пропорциональные соответствующим скоростям.
Действительно, обозначив эти отрезки через z1, z2, z3 и т. д.
|
|
Рис. 12. К графическому
дифференцированию
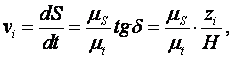
или, так как μs и μ t и Н величины постоянные, то скорость пропорциональна отрезкам zi:
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.