Методические указания к выполнению лабораторных работ с дисциплины "Основы расчета иконструирования машин и аппаратов пищевых производств", страница 15

где   - среднеарифметическое значение измеряемой величины

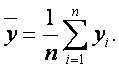                                                                              (6)

Появление того или иного значения  y_i  в интервале     

                                 

                                                                   (7)

 

а, следовательно, и появление соответствующего  абсолютной погрешности Δy_i.

Эта вероятность определяется законом нормального распреде­ления Гаусса.

3.4. Зависимость между случайными величинами. Понятия о корреляции и регрессии.

Между случайными величинами существует связь особого рода. При изменении одной величины (X) меняется распределение дру­гой (У ). Такая связь называется стохастической (корреляцион­ной).  Изменение случайной величины (У), соответствующее из­менению величины (X), разбивается при этом на две компоненты: стохастическую и случайную (связанную с влиянием собственных случайных факторов величин X и У). Если первая компонента отсутствует, то величины X и У независимы. Если же стохас­тическая компонента не равна нулю, то между X и У есть сто­хастическая связь. При этом соотношение между стохастической  и случайной компонентами определяет силу связи.

Оценка силы связи производится специальными критериями, причём важнейшим из них является коэффициент корреляции 

Он служит мерой силы линейной связи между двумя переменными X и У.

                                 (8)

Свойства коэффициента корреляции.

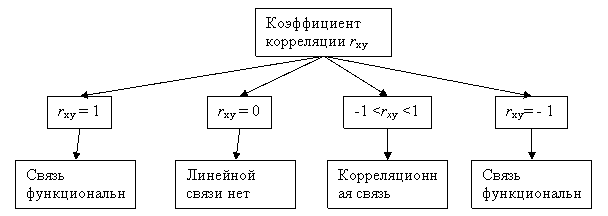
Если  r_xy = 0, то зависимость между величинами может иметь криволинейный характер (по параболе, экспоненте и т.д.). Значения  r_xy = ± 1 соответствуют строгой линейной связи меж­ду X и У . Коэффициент корреляции есть показатель того, на­сколько связь между случайными величинами близка к строгой линейной зависимости. Он одинаково отличает и слишком большую долю случайности, и слишком большую криволинейность этой связи.

Силу связи криволинейных зависимостей более эффективно можно оценить такой характеристикой, как корреляционное отло­жение, интерпретация которого не зависит от вида исследуемой зависимости  

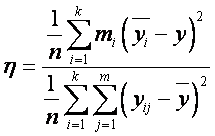          ,                                                          (9)

где числитель характеризует рассеяние частных средних 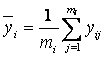 около своего общего среднего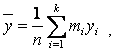    

а  знаменатель-дисперсия индивидуальных результатов наблюдения относительно общего среднего .

Регрессия. Коэффициент корреляции служит установлению значимости (неслучайности) изменения наблюдаемой случайной величины в процессе испытания. Не менее важным и необходимым при исследовании связей является установление формы связи между переменными, т.е. определение эмпирического уравнения, которым записывается связь у и х.

Вывод эмпирических уравнений (уравнений регрессии) распадается на два этапа: