Математическое моделирование. Динамические и статистические системы

          В динамических и стохастических системах главенствует причинность в лице необходимости. В статистических системах причинность реализует себя в форме случайности.

4.2 Динамические системы

          Динамические системы – системы, функционирующие на основе жестко детерминированных связей, когда на базе их анализа возможно однозначное описание поведения системы в прошлом, настоящем и будущем. Это системы, в которых сменяемость состояний четко регламентирована законами, проявляющимися в форме необходимых устойчивых взаимосвязей структурных компонентов системы. Состояние системы характеризуется вектором состояния  – где число параметров соответствует числу степеней свободы. Движение системы (ее развитие, эволюция) определено тогда, когда определены все компоненты вектора состояния.

          Как известно, уравнения движения системы могут быть приведены к виду:

          В более общем виде уравнения могут быть записаны в виде:

.

          В этих уравнениях 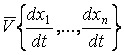 – вектор поля скоростей системы,  – вектор-оператор. Если поле скоростей не зависит от времени t явно, то система называется автономной. Цель которую ставит любой исследователь – найти зависимость состояний от времени, т.е. определить процесс изменения системы: определить вектор состояния . Если этот вектор состояния может быть найден, т.е. при соответствующих начальных и граничных условиях мы получим единственное решение (в смысле теоремы Коши), то в этом случае система называется голономной (интегрируемой). В противном случае, когда решение вообще не может быть получено в общем виде система называется неголономной. Классический пример голономной системы – задача Кеплера, задача о движении двух взаимно притягивающихся тел, неголономная система – система трех взаимно притягивающихся тел.

          В интегрируемой системе распределение энергии по внутренним степеням свободы остается либо неизменным, либо является периодически изменяющимся. В интегрируемых системах не происходит структурных перестроек.

          Интегрируемая система (в зависимости от степеней ее сложности) рано или поздно возвращается в исходное положение.

          Специфика поведения неголономных систем определяется не столько степенью их сложности, сколько характером внутренних взаимодействий. Общим для всех них является то обстоятельство, что при бесконечно малом изменении состояния системы число степеней свободы меньше, чем при конечном изменении состояния системы. Если система имеет n степеней свободы при конечных движениях и на нее наложено r неголономных связей, то при бесконечно малом изменении состояния она имеет всего n – r степеней свободы. Эти особенности неголономных систем наглядно проявляются в примерах колеса с узким следом или саней с короткими полозьями. Нельзя думать, что проблема неголономных систем вообще безнадежна. Существуют определенные подходы к анализу неголономных систем, они изложены в соответствующей литературе. Мы же обратимся к анализу тех систем, которые встречаются наиболее часто.

          В большей степени нас будут занимать нелинейные системы. Нелинейными называют системы, у которых поле скоростей содержит нелинейные компоненты относительно координат вектора состояния. Строго говоря, мир систем является нелинейным, поскольку нелинейность – свидетельство факта взаимодействия. Линейные системы – это идеализация реальности, на основе идеализации можно построить и нелинейные приближения.

          Ниже рассмотрены некоторые основные принципы составления математических моделей.