Математическое моделирование. Динамические и статистические системы, страница 9

          Тогда скорость изменения вероятности для вектора состояния  определится балансом вероятности:

.

          В случае статистической системы, состояния которой могут изменяться непрерывно, целью поиска является функция статистического распределения, имеющая смысл плотности вероятности состояния частицы в элементе фазового объема dГ

,

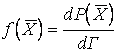где  –  вектор состояния системы, содержащейся внутри dГ.

          Если от вектора состояния дискретного перейти к вектору состояния непрерывному, то в этом пределе мы придем к уравнению Фоккера - Планка (или же его частным случаям).

          В числе частных случаев уравнения Фоккера - Планка можно указать уравнение диффузии 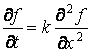   – для одномерного случая.

          Мы видим, что написанное уравнение по форме совпадает с уравнениями процессов переноса. Это обстоятельство является естественным, т.к. явления переноса имеют статистическую природу. Статистические методы исследования широко используются при интерпретации разных состояний и явлений в физике газов, жидкостей, твердых тел, для анализа ситуаций в сфере обслуживания, в задачах определения надежности.

          В качестве примера рассмотрим математическую модель формирования общественного мнения, предложенную Хакеном. В статистических и стохастических системах различают макро и микроскопические переменные. В качестве микроскопической переменной может выступить индивид. В качестве макроскопической единицы выступает социальная группа, придерживающаяся определенной ориентации. Пусть в большой социальной системе формируются два общественных полярных мнения, которые мы обозначим условно +, –. В качестве параметра порядка возьмем числа индивидов n₊ и n_- с соответствующими мнениями  +  и  –.  Формирование общественного мнения – кооперативный эффект. Каждый индивид находится под влиянием групп людей с противоположными мнениями.

          Значения n₊ и n_– являются случайными величинами, поэтому существует вероятность отличная от нуля, изменение мнения индивида с «+» на   «–»   и наоборот. Пусть  – вероятность изменения мнения индивида  с «+» на  «–»  в единицу времени, а  p_-+ (n+, n–) – вероятность изменения мнения с «–»  на  «+»  в единицу времени. Определяемой величиной, как и водится в статистической задаче является функция распределения вероятностей . Соответствующее кинетическое уравнение для функции  строится по стандартным рецептам физической и математической статистики. Мы ищем аналоги статистических систем, в которых имеет место столкновение двух противоположных тенденций, качеств. Такого рода аналог представляет собой кинетическое уравнение Больцмана и на основе его идеологии составим следующее уравнение:

          Для решения кинетического уравнения сделаем определенные предположения о величине р. Эти предположения включают в себя наличие определенного социального климата и воздействие внешнего влияния на отдельного индивида. Можно эти предположения представить в математической форме, видоизменив известную модель Изинга для ферромагнетика:

,

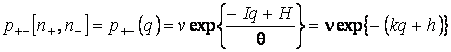где I – параметр адаптации по отношению к соседям, Н – параметр предпочтительности мнения, q – коллективный параметр общественного климата, n  – частота переходов + Û –, , .