Математическое моделирование. Динамические и статистические системы, страница 5

          Уравнение энергии примет вид:

.

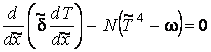          Граничные условия:

; ;

    ; .

          В развитие этой задачи можно поставить вопрос о конструкции ребра минимального веса. Речь идет о минимуме величины .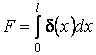

          Введем в рассмотрение безразмерную величину

.

          Произведем замену переменных по схеме

;

;

.

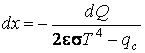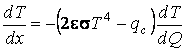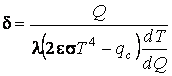и обезразмерив соответствующие параметры получим

.

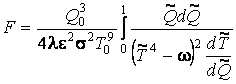          Уравнение Эйлера соответствующей вариационной задачи имеет вид

,

а его решением будет функция

.

          Константы С₁ и С₂ определяются из граничных условий:

,   ,   .

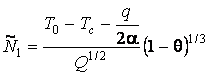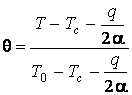          Расчет функционала дает: 

.

          Для теплоотводящего ребра , следовательно, для оптимального ребра Q = 1.

          Отсюда следует:

;   .

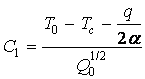          Для нахождения минимума функционала F решаем вариационную задачу для функции                              .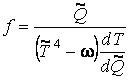

          Составим уравнение Эйлера для этой задачи:

,

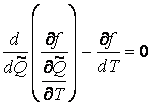имея ввиду, что в явном виде оператор

.

          Придем к следующим уравнениям:

;

.

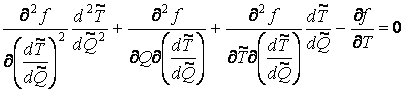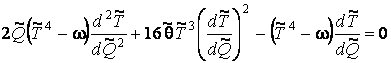          Наиболее простое решение соответствует случаю w = 0 (отсутствие источников тепла и дополнительного облучения):

.

          После расчета функционала получаем:

.

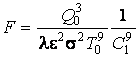          С помощью граничных условий находим

;   .

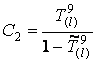          Наименьшему по весу излучающему ребру соответствует , что дает С₁ = 1; С₂ = 0; ; ; .

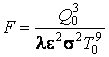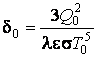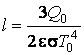          Для получения оптимального профиля ребра введем новые безразмерные величины:

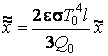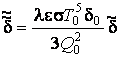;     и  .

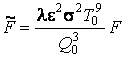          В безразмерных единицах