![]() ,
,
где ![]() – численность n-го поколения;
– численность n-го поколения;
![]() – численность
– численность ![]() -го поколения; множитель l характеризует пропускную способность среды.
И также известно уравнение Хатчинсона, определяющее динамику популяции с
эффектами последствия:
-го поколения; множитель l характеризует пропускную способность среды.
И также известно уравнение Хатчинсона, определяющее динамику популяции с
эффектами последствия:
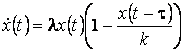 ,
,
где k выступает как стационарная характеристика популяции.
Оба приведенных выше уравнения являются нелинейными. Как известно, фактор нелинейности значительно расширяет спектр возможных решений. Детальное исследование систем с запаздыванием показывает, что наличие запаздывания может приводить к детализации состояния системы, поэтому в таких случаях исследование системы на устойчивость приобретает особую актуальность.
Исследование на устойчивость позволяет выделить область управляющих параметров функционирования системы, при которых возможны стационарные решения.
Задачи с запаздыванием резко усложняются при наличии нескольких запаздываний, распределенных, случайных запаздываниях или же их комбинациях.
Несмотря на то, что любая модель значительно беднее по содержанию, чем сама описываемая система, тем не менее на языке математики удается отразить все многообразие, укомплектованность окружающего нас мира: органическое единство необходимого и случайного, дискретного и континуального, универсальность взаимодействий, скрытый внутренний потенциал природы к саморазвитию.
Физика и математика XX-го века сыграли выдающуюся революционную роль в смене сложившихся стереотипов научного мышления. Акцент научных исследований сделан на анализе нелинейных систем. Такие понятия как бифуркации, странный аттрактор, солитон сейчас стали обычными «расхожими» понятиями как и основные понятия классической механики. При этом следует иметь в виду, что часто бывает так, что поразительный новый результат следует из современного прочтения классических уравнений физики. Так это произошло при внимательном анализе известных результатов гидро-газодинамики, приведшем к фундаментальным открытиям целого класса систем с динамическим хаосом. В своих работах Пригожин и Хакен показали насколько многообещающим является мир нелинейных систем.
Одним из важнейших феноменов этого мира являются проявление кооперативных эффектов в самоорганизации нелинейных систем. Исследование явлений самоорганизации является предметом выделившейся в конце 20-го века науки – синергетики. Ее методы являются общими для термодинамики, биохимии, астрофизики, социально-экономических систем и т.д. Их использование требует значительной специальной подготовки.
В качестве примера динамической задачи приведем расчет излучающего ребра теплообменника с наименьшим весом. Пример заимствован из [34].
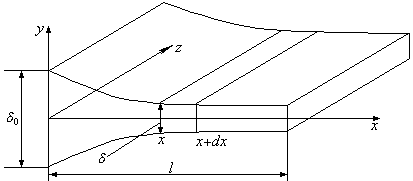
Рис. 14. Схема излучающего ребра
Исходные
данные: ![]() ;
; ![]() .
.
Степень черноты и все физические характеристики считаются не зависящими от координат и температуры. Контур ребра считается достаточно пологим.
Уравнение энергии имеет вид:
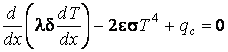 ,
,
где l – коэффициент теплопроводности; e – степень черноты;
![]() Вт/м2К4 –
постоянная Стефана – Больцмана; Т – абсолютная температура; qc
– характеристика источников тепла.
Вт/м2К4 –
постоянная Стефана – Больцмана; Т – абсолютная температура; qc
– характеристика источников тепла.
Перейдем к безразмерным переменным
![]() ;
; 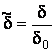 ;
;
 ;
; 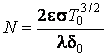 ;
;
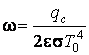 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.